Squared Squares
There are 4 main kinds of squared squares which have been of sufficient interest to be searched for, counted and recorded; That is, the three types depicted below, and the fourth type, Mrs Perkin's Quilts, which can include those three types and in addition, squared squares which are 'imperfect' and 'compound' as well. All four kinds of squared square have the squares in the dissection (the 'elements') reduced by any common factor so their GCD (greatest common divisor) = 1.
Simple Perfect Squared Squares (SPSSs) are defined as Simple by having no smaller squared squares or squared rectangles in the dissection. and Perfect if the squares are all different sizes. They are considerably rare compared to perfect simple squared rectangles of the same order . According to David Gale[1], "Bouwkamp says that there are about 5,000,000 perfect simple squared rectangles to every such [squared] square (for order greater than 20)!". The lowest order SPSS appears alone in order 21.
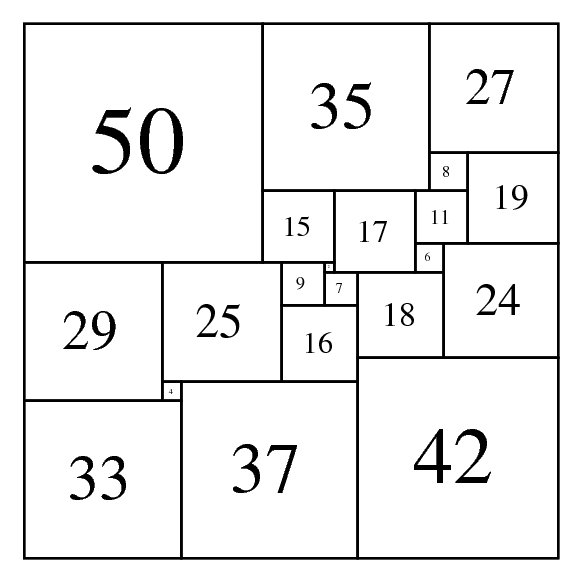
SPSS (Simple Perfect Squared Square), Order 21: 112 x 112 (AJWD)
Simple Imperfect Squared Squares (SISSs) are Imperfect as not all the squares are different sizes (at least two squares are the same size). These are more numerous than Simple Perfect Squared Squares. The first one appears in order 13. Having squares of the same size can result in SISSs having symmetrical arrangements. SISSs can be used to 'derive' SPSSs two orders down.
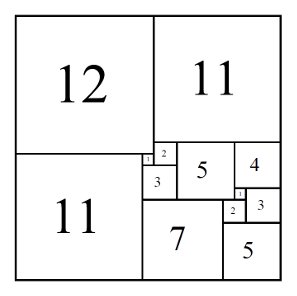
SISS (Simple Imperfect Squared Square), Order 13: 23 x 23
Compound Perfect Squared Squares (CPSSs) are defined as Compound if there is a rectangle or a smaller dissected square in the dissection. At lower orders these squared squares are rarer (after ignoring all symmetries) at any given order (>= 24) than SPSSs.
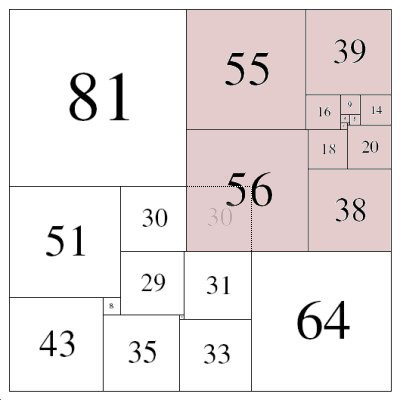
CPSS (Compound Perfect Squared Square), Order 24: 175 x 175(THW)
The chronology of the significant squared square dissection discoveries spans from the year 1902 to present time. Over time the frequency of the discoveries has increased. In 2013 alone there were 8 new developments. In an anecdotal sense, much has changed in the past 100 years of discoveries. Originally mathematicians read about new puzzles in published work or in the case of Lady Isabel's Casket in the London Magazine. In modern times information can travel much quicker using email, conference call, and websites such as this.
A chronology of the significant square dissection discoveries and the people who made them;
- 1902 H.E. Dudeney published a puzzle called Lady Isabel's Casket that concerns the dissection of a square into different sized squares and a rectangle. According to David Singmaster 'Lady Isabel's Casket' appeared first in The London Magazine. 7 (No. 42) (Jan 1902) 584 & 8 (No. 43) (Feb 1902) 56. Square into 12 unequal squares and a rectangle (Singmaster 5.J. SQUARED SQUARES, ETC.). This is the first published reference dealing with the dissection of a square into smaller different sized squares. It was also published in The Canterbury Puzzles in 1907.
- 1903 M. Dehn studied the squaring problem in 1903 and proved;
- A rectangle can be squared if and only if its sides are commensurable. [It follows a squared rectangle can always be given integer sides]
- If a rectangle can be squared then there are infinitely many perfect squarings.
- 1907-1914 S. Loyd published The Patch Quilt Puzzle. A square quilt made of 169 square patches of the same size is to be divided into the smallest number of square pieces by cutting along lattice lines. The answer, which is unique, is composed of 11 squares with sides 1,1,2,2,2,3,3,4,6,6,7 within a square of 13. It is neither perfect nor simple. Gardner states that this problem first appeared in 1907 in a puzzle magazine edited by Sam Loyd. David Singmaster lists it as first appearing in 1914 in Cyclopedia by Loyd but credits Loyd with publishing Our Puzzle Magazine in 1907 - 08. This puzzle also appeared in a publication by Henry Dudeney as Mrs Perkins Quilt. Problem 173 in Amusements in Mathematics. 1917
- 1923-24 Z. Moroń started work on the problem of squaring rectangles and squares. "S. Ruziewicz communicated to us (Z. Moroń and W Orlicz) the problem of the dissection of a rectangle into squares. He had heard it from the mathematicians of the University of Krakow who took an interest in it." Moroń later claimed in a paper, translated by Dr Dobrzycki "I also knew of the dissection of a square which was later given by R Sprague. Neverless I did not publish ..." (Skinner, Who's Who, & What's What p 9).
- 1925 Z. Moroń published a paper, 'On the Dissection of a Rectangle into Squares' (translated from Polish). Moroń gave the first examples of rectangles divided into unequal squares in his paper. He doesn't indicate how they were obtained. Rectangle I is 33 x 32 in size and is divided into 9 unequal squares. Rectangle II is 65 x 47 and has ten squares. Moroń raised the question "For what squares is it possible to dissect them into squares?" He then observes “if there exists a rectangle (of different sides) for which there are two dissections R1 and R2 such that;
- in neither of these dissections does there appear a square equal to the smaller side of the rectangle and,
- each square of dissection R1 is different from each square in dissection R2, then the square is dissected into squares, all different
- 1930 M. Kraitchik published a personal communication from N. Lusin which stated it was impossible to dissect a square into a finite number of different elements.
- 1931 M. Abe, working in isolation in Japan published his first paper on squared rectangles, he produced over 600 squared rectangles apparently in search of perfect squared squares. He published a second paper in 1932.
- 1934-35 A.H. Stone hears about the problem, and later communicates it to R.L. Brooks, C.A.B. Smith, and W.T.Tutte. According to C.A.B. Smith (1990 correspondence to Skinner). "Prof. W.R. Dean is largely responsible for the development of the idea of squaring the square - he visited Arthur Stone's school before Arthur came to Cambridge and said that an unsolved problem was to show that a square can not be dissected into a finite number of unequal squares.". W.R. Dean's visit to Arthur Stone's school was after Erdős's visit to Trinity College early in October 1934. So Stone probably didn't hear about the problem before then.
- 1935, July. Professor Stanislaw Ruziewicz posed the problem, "Can a square be dissected into different squares?"as Problem 59 in the Scottish Book
- 1939 R.P. Sprague published his solution to the problem of squaring the square. Sprague constructed his solution using several copies of various sizes of Z. Moroń's Rectangle I (33x32), Rectangle II (65x47) and a third 12 order simple perfect rectangle and five other elemental squares to create an order 55, compound perfect squared square (CPSS) with side 4205.
- 1939 March; A. Stone's lecture: "Squaring the Square" announces Brooks's example with 39 elements, side 4639, but containing a perfect subrectangle. Minutes of the 203rd Meeting of the Trinity Mathematical Society (Cambridge) (13 Mar 1939). Minute Books, vol. III, pp. 244‑246.
- 1939 April; Announcement by C.A.B. Smith that Tutte had found a perfect squared square with no perfect subrectangle. Minutes of the 204th Meeting of the Trinity Mathematical Society (Cambridge) (24 Apr 1939). Minute Books, vol. III, p. 248.
- 1940 R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T.Tutte published 'The Dissection of Rectangles into Squares" (1st page only), referring to an order 55 SPSS, side 5468 using theoretical methods involving the use of symmetry in electrical networks, attributed to all four authors and an empirically constructed order 26 CPSS, side 608, attributed to Tutte. In the same year A.H. Stone uses 2 order 13 SPSRs as R1, R2 to construct and publish a Moroń dissection CPSS of order 28, side 1015.
- 1946-7 C.J. Bouwkamp, published 'On the dissection of rectangles into squares', 'Paper I', 'Papers II and Paper III' and 'On the construction of simple perfect squared squares' (Koninkl. Nederl. Akad. Wetensch. Proc. Ser. A)
- 1948 T.H.Willcocks, discovered a CPSS side 175, of order 24. It is one of 4 isomers (squarings with the same elements), since the subrectangle has 4 possible orientations. He also published two new CPSSs in order 27, with sides 867 and 849, and a new CPSS in order 28 with a side of 577.
- 1950 R.L. Brooks discovery of a simple perfect squared square (SPSS), side 4920 of order 38 was published by W.T. Tutte in 1950. A number of higher order PSSs were also published in this paper including a CPSS of order 85, side 227807876, constructed from two rectangles produced using rotor-stator theory, he mentions a perfect squared square of the 29th order which has reduced side 1424, the Bouwkampcode is misformed so this must be an error or misprint as only one order 29: 1424 SPSS (no CPSSs) exists and it has different elements. The two CPSS of side 1015 order 28 and a third of order 28 and side 1073 are given. CPSSs of order 39 are given one with side 1813 (by the Trinity Four) and one with side 4639 due to Brooks. A SPSS of the 52nd order, due to Tutte and Smith is given, as is one of 70th order and side 384948 and the 69th order with a side of 7919535. The paper was submitted 18 March 1948.
- 1951 T.H.Willcocks, published 'A note on some perfect squared squares', his account of the methods he used to construct CPSSs with small sizes. He included a number of new squared squares, these included his discovery of a new CPSS of order 26 with side 492, and 2 new CPSSs of order 27 with sides 872 and 890.
- 1958 M. Gardner published an article in Mathematical Games, Scientific American magazine November 1958 on squared squares written by William Tutte.
- 1959 "The smallest published square that is both simple and perfect is a 38th-order square with a side of 4,920, discovered by R.L. Brooks. In 1959 this was bettered by T.H. Willcocks of Bristol, with a 37th-order square, 1,947 on the side. The addendum (pp. 162-4) to Tutte's chapter in Martin Gardner's "More Mathematical Puzzles and Diversions"
- 1960 C.J. Bouwkamp, A.J.W. Duijvestijn, P. Medema [7] Enumerated all the polyhedral graphs up to 15 edges to produce simple perfect and simple imperfect squared rectangles (SPSRs & SISRs) to order 14.
- 1962 A.J.W. Duijvestijn, in his PhD thesis 'Electronic Computation Of Squared Rectangles', showed no SPSS exists with fewer than 20 squares.
- 1963 R. Ellis produced a 2x1 non-trivial compound squared rectangle 282 x 564 of order 25
- 1964 C.J. Bouwkamp, A.J.W. Duijvestijn, J. Haubrich, publish a catalog of SPSRs orders 9 to 18.
- 1963 P.J. Federico published 2 CPSSs of order 25 (with sides 235 and 344). His paper also gave 3 CPSSs of order 26, 12 CPSSs of order 27, 17 CPSSs of order 28, 1 CPSS of order 29, 1 of order 30 and 1 of order 37. Many of these CPSSs were new and a detailed account of the construction techniques used to construct them was given.
- 1964 J.C. Wilson found an SPSS with side 503 of order 25.
- 1965-66 E. Lainez constructed 2 CPSSs with sides 360, 460 of orders 26 and 27 respectively.
- 1966 T.H. Willcocks constructed 2 SPSSs with sides 1415, 2606 of order 31.
- 1967 G.H. Morley's SPSS method published in Eureka. Eight examples, from 56:1118251A to 60:5629849A, can be found here. They include 60:616457A, wrongly stated in the article to have side 616,467.
- 1967 T.H. Willcocks constructs 2 SPSSs with sides 1360, 1372 of order 31.
- 1967 J.C. Wilson included in his PhD thesis 5 new SPSSs of order 25 (including the one he found in 1964) and 24 new SPSSs of order 26.
- 1968 I.M Yaglom published the first book How to Dissect a Square on squared rectangles and squared squares (in Russian).
links to book; djvu (1.7M) or pdf (9.5M).- 1969 T.H. Willcocks constructed an SPSS with side 900 of order 27.
- 1972 N.D. Kazarinoff and R. Weitzenkamp proved the nonexistence of a CPSS of order less than 22.
- 1978 Mar, A.J.W. Duijvestijn, SPSS order 21 enumerated; 1 SPSS (21 : 112 x 112) proved order minimal and unique.
- 1978 A.J. W. Duijvestijn found an SPSS side 110 of order 22. T.H. Willcocks was able to transform it into a different SPSS with side 110 of order 22. By Gambini's result these are the smallest size perfect squared squares.
- 1982 A. J. W. Duijvestijn, P. J. Federico, P. Leeuw established the lower limit of the order of CPSSs and searched to find all that can exist up to and including order 24. The main results were; There are no CPSSs below order 24. and there is one and only one (THW 24:175) CPSS of order 24.
- 1983 A. Augusteijn and A. J. W. Duijvestijn publish 'Simple Perfect Square-Cylinders of Low Order' and find 2 simple perfect square-cylinders with sides 79 and 81 of order 20
- 1990 J.D. Skinner constructed SPSSs of side 180 and side 188 of order 23.
- 1990 C.J. Bouwkamp constructed 2 SPSSs of order 24 of side 186 and side 288 of order 24.
- 1991 Jul, A.J.W. Duijvestijn enumerated the remaining SPSSs and 2x1 SPSRs of orders 21 - 24.
- 1992 Jan, C.J. Bouwkamp constructed 5 SPSS of order 25 and 21 SPSS of order 26.
- 1992 A.J.W. Duijvestijn enumerated the remaining SPSSs of order 25 and 2x1 SPSRs and published SPSSs of orders 21 to 25
- 1993 J.D. Skinner found 3 SPSSs of order 26.
- 1993 S. J. Chapman published 'The dissection of rectangles, cylinders, tori, and Möbius bands into squares.'
- 1993 J.D. Skinner published "Squared Squares, Who's Who & What's What"
- 1996 A.J.W. Duijvestijn enumerated the remaining SPSSs and 2x1 SPSRs of order 26.
- 1999 I. Gambini published his doctoral thesis 'Quant aux carrés carrelés' on squared squares. Using the 'classical' graph-electrical method he confirmed Duijvestijn's counts of SPSSs up to order 26. He also found the known CPSSs up to order 26. With packing algorithms based on new bounds for placement of small squares on boundaries he obtained more than 30,000 squared squares and proved the 110 SPSSs as the smallest possible perfect squared squares. He also found solutions to two closely related problems; the decomposition using distinct sized squares of the cylinder and of the torus. He also published a paper 'A method for cutting squares into distinct squares' (Discrete Applied Mathematics 98 (1999) 65-80)
- 2003 J.D. Skinner completed enumeration of SPSSs of order 27. Skinner also enumerated 97% of order 28 SPSSs and significant amounts of order 29 and 30, and a variety of CPSSs in low and higher orders.
- 2003 S.E. Anderson, using plantri and software he wrote, found 60 SPSSs of order 28
- 2007 G.H. Morley published 130 SPSSs of order 31.
- 2010 S.E. Anderson and Ed Pegg Jr. enumerate all SPSSs and CPSSs up to order 28. They confirm that the known SPSSs up to order 27 are complete, and find the remaining 30 of a total 3001 SPSSs of order 28.
In counting isomer classes of CPSS they find;
- 1 CPSS of order 24, with 4 isomers. The well known Willcocks square with side 175, published in 1948. Duijvestijn, Federico and Leeuw proved this CPSS was unique to the order in 1982.
- 2 CPSSs of order 25, with 12 isomers. There are 2 CPSSs of order 25, with sides 235 and 344, found by Federico, and published in 1963, but no one knew if the order was completely enumerated. The enumeration of this order is now finalised.
- 16 CPSS of order 26, with 100 isomers, including 1 CPSS with side 512 not previously known ( 8 isomers), but which appears to have been produced, but not published in 1982 by Duijvestijn, Federico and Leeuw. The enumeration of this order is now complete.
- 46 CPSSs of order 27, with 220 isomers, including 7 CPSSs not previously known, 3 of which appear to have been earlier discoveries by Duijvestijn, Federico and Leeuw in 1982. The 46 CPSSs completes the enumeration of this order.
- 143 CPSSs of order 28, with 948 isomers, including 50 CPSSs not previously known, 13 of these have been attributed to Duijvestijn, Federico and Leeuw from 1982. The 143 CPSSs completes the order.
- 2011 August S.E. Anderson, and Stephen Johnson finalise SPSSs and SISSs of order 29. They found a total of 7901 SPSSs and 326037 SISSs in order 29.
- 2011 October, Stephen Johnson discovers 500+ SPSSs and 60 or so CPSSs from order 30 to order 36.
- In January 2012 a duplicate was detected in order 29 SPSSs, all tilings were regenerated from the graphs and a new count was done. The total for order 29 SPSS was adjusted down to 7901. This was incorrectly reported by Stuart Anderson as 7902 SPSSs until 2012. Order 28 SPSSs were also recounted in January 2012 and the total of 3001 was reconfirmed.
- In January 2012 Geoffrey Morley finds 31 new CPSSs in orders 30-34.
- In April 2012, Lorenz Milla completed searches of the 13 and 14 vertex, 31 edge polyhedral graph classes, using Stuart Anderson's noddy (node analysis on electrical nets) software and found 61 new SPSSs of order 30 (there are all up 75 SPSSs derived from the 31 edge, 14 vertex graphs, and none from the 31 edge, 13 vertex graphs).
- In May 2012 Stuart Anderson and Thom Sulanke collaborated to re-investigate squared cylinders. The investigation by Anderson and Sulanke establishes that there are 18 Simple Perfect Squared-Cylinders (SPSCs) in order 20, 16 were new discoveries and were all 80x80 in size and can be obtained by combining two cyl-nets and so were not found by Augusteijn and Duijvestijn. This confirms that order 20 is the lowest order in which SPSCs can appear, and that the 79x79 SPSC found by Augusteijn and Duijvestijn in 1983 is the smallest size in the lowest possible order .
- In October/November 2012 Stuart Anderson uses the Amazon EC2 supercomputer to enumerate CPSSs of order 29. He finds 412 CPSSs and 2308 CPSS isomers
- 2013 January and February; James Williams wrote a program which he ran for 6 weeks which produced over 15 million SPSSs from orders 21 to 44. The software was not exhastive, it did not find all SPSSs in a given order, the goal was to find as many perfect squares as possible in a practical amount of time. No particular effort was made to search for a particular kind of square ( low order, etc. ) but rather just to find the most. His algorithm looks for squares for which the associated electrical network can be cut roughly in half by cutting at exactly three nodes. The resulting two halves are connected together in a squared square. A number of tests or 'filters' are used to evaluate whether a pair of networks will form a perfect square and these tests speed up the processing considerably. This collection, the 'Williams Collection', is currently being added to the site, beginning with order 30 (no new discoveries were found below order 30).
- 2013 March, June; Stuart Anderson publishes (March) to the Arxiv and updates (June) a paper on 'Compound Perfect Squared Squares of the Order Twenties'.
- 2013 March and April; Lorenz Milla and Stuart Anderson enumerated simple squared squares of order 30. Lorenz used plantri (McKay/Brinkmann) to generate graphs, and Stuart Anderson's sqfind to find squared squares and his sqt to encode the dissections. Lorenz ran the programs on 17 dual core computers over the Easter school holidays. Some 6756 new SPSSs were found, combined with the known 13810 SPSSs of order 30 (including 9189 SPSSs found in Jan/Feb 2013 by James Williams) there are 20566 order 30 SPSSs in total. Simple Imperfect Squared Squares (SISSs) of order 30 were also enumerated. The total for order 30 SISSs is 667403. A total of 193130 order 30 (Compound Imperfect Squared Squares) CISSs was also found - unlike the SPSS and SISS counts, the CISS count is not a complete enumeration.
- 2013 May, Lorenz Milla and Stuart Anderson enumerate CPSSs of order 30. Lorenz processes 13, 14, and 15 vertex, 2-connected, minimum degree 3, 31 edge graphs of order 30 (8,377,405,224 graphs), then Stuart and Lorenz process half each of the 16 vertex, 2-connected, minimum degree 3, 31 edge graphs (35,873,044,824 graphs) to find 941 CPSSs, with 5668 CPSS isomers in order 30. Stuart and Lorenz both wrote new software; Stuart implemented a technique of Tutte's, used by Duijvestijn in his thesis, that factors the Kirchhoff matrix determinant of a graph into a product of 3 numbers as follows; 2, a square free number and a square number (this is a necessary condition for a graph to produce a squared square). This method resulted in a 3x speed up of the search. This part of the search was implemented as a program called sqfree, available on the downloads page. Lorenz also produced new software to produce the all isomers of the most common types of CPSSs and identify the canonical tablecode representative from the isomers of a CPSS.
- 2013 June, July, August; Lorenz Milla and Stuart Anderson rewrote Stuart's software to improve the efficiency of the determinant factorisation technique recommended by William Tutte in his writings to speed up squared square searches. Lorenz replaced the Boost library with C arrays and handwritten linear algebra routines; LU decomposition was replaced with LDL decomposition (planar maps are symmetrical, so LDL Cholesky decomposition is possible and twice as fast as LU decomposition). Lorenz also wrote a plantri plugin to filter graphs using the determinant factorisation technique as they were produced, he was also able to speed up the routines in Stuart's, sqfind and sqt programs and combine the plantri plugin and sqfind into a single program mandrill (a combination of the names Milla and Anderson). The end result was squared square software 35 times faster than what was used several months ago. This made it possible to complete the enumeration of order 31 and 32 compound perfect (CPSSs), simple perfect (SPSSs) and simple imperfect squared squares (SISSs) in under 2 months. The computations were done by Lorenz on his computers. There are 54541 SPSSs in order 31 and 144161 SPSSs in order 32. There are 17351 order 31 CPSS isomers and 2788 order 31 CPSSs (isomer classes), 52196 order 32 CPSS isomers and 7941 order 32 CPSSs (isomer classes).
- 2013 August. A recent (August 2013) paper by Ed Wynn extends the exhaustive generation of all squared square dissections, having relatively prime sides (Mrs Perkins's quilts) up to order 18, using the plantri software with a graph theoretical approach which is different to the electrical network method of BSST/Duijvestijn. The results were cross-checked by generating all dissections of small sizes using Knuth's dancing links algorithm to produce exact cover square dissections. In the paper's appendix, Ed lists values from several sequences in the OEIS with previously known values that have been confirmed in the current work (or, conversely, have been used to check the current work). See Mrs Perkins's quilts. The great majority of squared square dissections produced by Ed Wynn are CISSs (compound imperfect squared squares), as only a handful of simple squared square dissections exist below order 18, and perfect squared square dissections only begin at order 21.
- 2013 September. A second run, conducted in September 2013 by Lorenz Milla and Stuart Anderson was necessary due to a bug in the determinant factorisation routine which affected a small number of cases. The second run resulted in some changes in the SISS totals, there are actually 1627218 SISSs in order 31 and 3508516 SISSs in order 32. There was no change to the SPSS or CPSS totals.
- 2013 December ; Stephen Johnson collated the results of his squared square searches in early 2013 and made them available. A number of new CPSS and SPSS discoveries in orders 33-37 were found, these have been included in the website.
- 2014 March Brian Trial uses a new 'Ell-Munch' method to find PSSs in orders where there are large gaps in the current catalogues. By “ell,” we mean any six-sided figure whose sides are parallel to the coordinate axes (Henle 2008). Brian's lowest order find is of order 34 and the highest is order 236. He wrote;
There are 4 different types of Ell depending on what quadrant the cut out section is located, which could have any rectangular shape, some quite stretched in one direction as we can see in the solutions so far. Another "munch" can be done along any one of the 6 sides of the Ell depending on the sides' relative sizes.His method produces some large squares including several with exact sizes of 10^6, 10^7 and 10^8. With this method he finds 114795 new PSSs, we call these the 'Trial collection', in orders 34-236.- 2014 April. Jim William enumerated all CPSSs (and isomers) up to order 36. Jim wrote new software to implement a substitution method, similar to Duijvestijn, Federico and Leeuw (1982), but with significant modifications to speed up the search. A outline of the method, by Jim;
"The idea was to enumerate “almost perfect squares” or APSs which consist of a square subdivided into a number of smaller squares, each of different size, plus [at least] one rectangle. Then cross check this with a list of perfect rectangles to find combinations that create a perfect square. I think using this technique it should be easy to enumerate all compound perfect squares up to order 36, and with some significant compute effort probably up to somewhere in the 38-40 range."
Initials of person attributed CPSS discovery & totals Order 33 Order 34 Order 35 Order 36 SEA 1 0 0 225 S_J 12 16 7 3 C_M 1 1 1 1 CJB 9 18 0 2 PJF 44 11 13 0 THW 7 1 0 0 GHM 296 141 0 2 M&A 641 415 97 37 JBW 2013 7016 4 13 27 Total in 2013 8027 607 131 297 JBW 2014 14386 61666 172199 466211 JBW 2013 & 2014 21402 61670 172212 466238 Complete CPSS class total
(right click & save link as a zipped postscript file for a booklet of the CPSSs)22413 62273 172330 466508 Complete CPSS isomer total
150669 429458 1206181 3337989 - 2014 May June ; Jim Williams, with new software enumerated SPSSs of order 33. In 2 weeks he found 378197 SPSSs.
- 2016 April ; Jim Williams, enumerated SPSSs of order 34 and order 35. There are 990981 SPSSs in order 34 and 2578081 SPSSs in order 35.
Updated on ... 1 May, 2016