Order 25 Compound Perfect Squared Squares (CPSSs)
There are only 2 CPSSs in order 25. Both these CPSSs were originally found by P. J. Federico in 1962.
- tablecode (2) CPSS; Order 25 cpsso25.txt
- boukampcode (2) CPSS; Order 25 cpsso25.bkp
- (2) CPSS; Order 25
 cpsso25.pdf
cpsso25.pdf - (12) CPSS isomers ; Order 25
 cpsso25-isomers.pdf
cpsso25-isomers.pdf
A detailed account of the construction methods he used are given in the 1963 paper 'A note on some low-order perfect squared squares'
In this paper Federico describes a variety of methods of forming low-order squared squares, and gives a list of 35 solutions. The methods are named as;
- Method 1. Two rectangles.
- Method 2. Two rectangles and one square.
- Method 3. Two rectangles and two squares.
- Method 4. Two rectangles and three squares.
- Method 5. Modified simple rectangle.
- Method 6. Modified imperfect rectangle.
- Method 7. Simple deficient perfect squares.
- Method 8. Squared hexagons with two opposite sides equal.
In method 6, he describes the construction of what he called a 'deficient' perfect square. He is able to combine this with a perfect rectangle from the catalog to create a CPSS of order 25, with a side of 235 and a subrectangle 111 x 94.
Construct what might be called a deficient perfect square. This is a square which is divided into smaller squares, all different, and one rectangle. The same simple method, described in (12) and elsewhere, for constructing perfect rectangles can be used. First sketch a rectangle cut up into smaller rectangles. Imagine all of these rectangles except a corner one to be squares and work out what the relative sizes of the squares must be. Thus in Figure 4 the side of one small square is designated by x and of an adjoining square by y; the
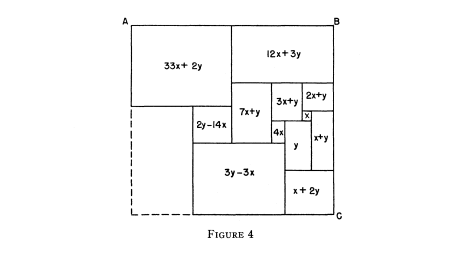
Figure 4
sides of the other assumed squares can be computed from these two, except the lower left-hand corner, shown in dotted lines, is not assumed to be a square. Then the sum of the sides of the component squares along AB is set equal to the sum of the sides along BC in order to make the whole figure a square. This gives the equation 2y = 29x, and x can be taken equal to 2 and y to 29. The result is a square of side 235 divided into 12 different squares and one rectangle 94 X 111, discernible in Figure 5.
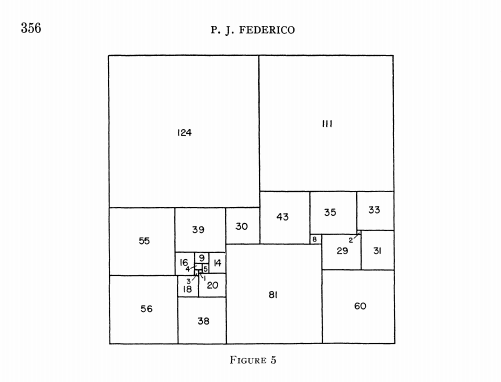
Figure 5; 25 : 235a PJF 1962
After a deficient perfect square is found, the next step is to see whether there is a perfect squared rectangle (including compounded rectangles) of the same shape as the single rectangle of the deficient square, to be fitted in to form a complete squared square. This is done from the tables of simple perfect squared rectangles. For the example given, there is a 94 X 111 simple squared rectangle that fits; no component squares are duplicated and a perfect square of order 25 and side 235 is formed (number 2 in the list). Incidentally, it may be noted that the included squared rectangle (which also appears in other squares) is the same as that in the 24-order perfect square.
Federico found another order 25 CPSS of size 344 using a variation of deficient squares given in Method 7. It the only other CPSS of this order.
Method 7. Simple deficient perfect squares. Some of the déficient perfect squares could not be reduced to the other figures mentioned in the preceding paragraph, or to the figures mentioned in the following paragraph; these might be called simple deficient perfect squares. The 25-order perfect square numbered 3 in the list, and shown in Figure 6, is a result. The rectangular space to be filled is 97 X 193, which is reduced to 96 X 97 by inserting a square of side 97 and filled by Pn(96, 97).
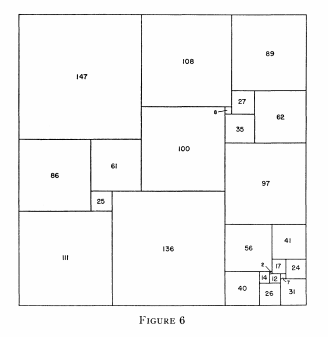
Figure 6; 25 : 344a PJF 1962
Federico had found both of the two and only CPSSs of order 25, though he did not know he had exhausted the discoveries of this order, and it was not proved until Gambini's thesis was published in 1999.