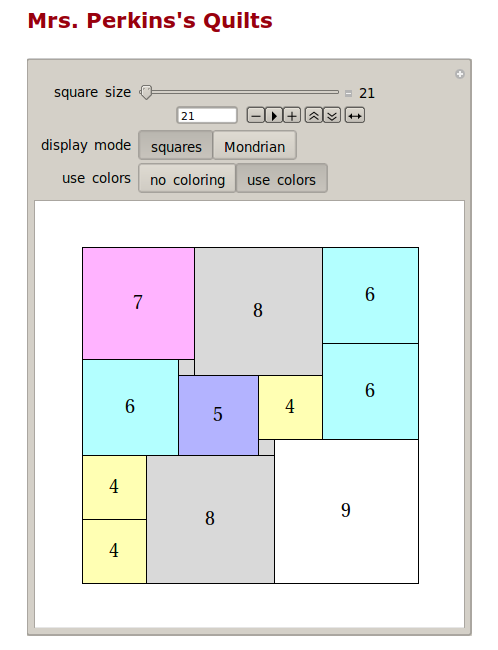
Mrs Perkins's Quilt

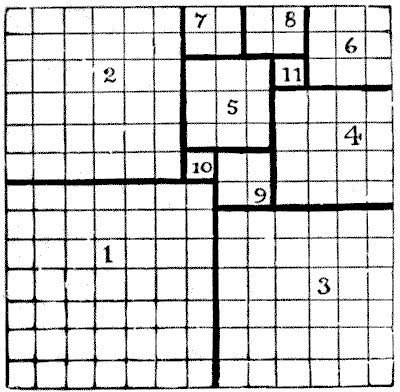
Mrs Perkins's Quilt

Mrs Perkins's Quilt Solution

(numbering indicates the different patches, not their sizes)

"For Christmas, Mrs. Potipher Perkins received a very pretty patchwork quilt constructed of 169 square pieces of silk material. The puzzle is to find the smallest number of square portions of which the quilt could be composed and show how they might be joined together. Or, to put it the reverse way, divide the quilt into as few square portions as possible by merely cutting the stitches."

Henry E. Dudeney

Sam Loyd published The Patch Quilt Puzzle. A square quilt made of 169 square patches of the same size is to be divided into the smallest number of square pieces by cutting along lattice lines. The answer, which is unique, is composed of 11 squares with sides 1,1,2,2,2,3,3,4,6,6,7 within a square of 13. It is neither perfect nor simple. Gardner states that this problem first appeared in 1907 in a puzzle magazine edited by Sam Loyd. David Singmaster lists it as first appearing in 1914 in Cyclopedia by Loyd but credits Loyd with publishing Our Puzzle Magazine in 1907 - 08. This puzzle also appeared in a publication by Henry Dudeney as Mrs Perkins's Quilt. Problem 173 in Amusements in Mathematics. 1917

Define a quilt as a square made from smaller integer squares. The order of a quilt is the number of smaller squares. The size is the edge length of the full quilt. It is impossible to dissect the 13×13 square into fewer than 11 squares, so this dissection is optimal. An additional constraint is that the side lengths cannot have a common factor. Any optimal quilt is a Mrs. Perkins's quilt. A primitive quilt is one without any sub-quilts, or is not substantially derived from a smaller quilt. The primitive quilts are not necessarily optimal quilts.

Richard K. Guy, the maintainer of Unsolved Problems in Geometry lists optimal quilts as problem C3. As of January 7, 2003, this web page article from Ed Pegg Jr shows (in bold face) the listing of the lowest known order for a given square of size n. The first value in each bracketed list is the order. The following values are the sizes of quilts that first appear in that order. We reproduce the listing here;

Two obvious sequences can be obtained from this data;

Sequence A089046 ; "Least edge-length of a square dissectable into at least n squares in the Mrs Perkins's quilt problem.", lists the optimal quilts as the lowest known size for a given square of order n.
Sequence A089047 ; "Greatest edge-length of a square dissectable into up to n squares in the Mrs Perkins’s quilt problem.", lists the quilts with the greatest known size for a given square of order n.

Ed Pegg writes; "The above list can be attacked in two ways -- computer programs and hand analysis. Dozens of improvements were discovered by Richard Guy, Lance Gay, and Geoff Morley." Quilt construction techniques have been developed by Ed Pegg, Richard Guy and Lance Gay. Programs to search for quilts have been written by Antony Boucher and Lance Guy. Mathematica code has been written to display quilts by Ed Pegg Jr.

In 2010, Richard Guy suggested to Ed Pegg Jr that they compile all their findings and methods for a paper. Many of the larger optimal quilts were identified by Geoffrey Morley, from publications on squared squares by Duijvestijn. As Duijvestijn and Bouwkamp are no longer with us, Ed Pegg sought assistance from Stuart Anderson, who wrote some new software for finding squared squares and quilts. After Pegg and Anderson ran the computer programs for a number of months, perfect squares for orders up to 28 and a large portion of order 29 were explored, along with a complete listing of imperfect squared squares up to order 28. A number of new discoveries were made in the compilation process. While order 28 was being compiled, Ed updated the optimal quilts to order 27.

The above listing forms the basis of a Mathematica Demonstration by Ed Pegg Jr and Richard Guy;

Mrs Perkins's Demonstration

Optimal Mrs Perkins's Quilts Demonstration

After including the results from orders 28 and 29 perfect and imperfect squared squares, along with some inclusions from Ed Pegg, Stuart Anderson has updated the list;

In addition to including entries for order 28 and 29, 1099 and 1165 were included in order 27 and 847 was included in order 26.

In March/April 2013 Lorenz Milla and Stuart Anderson enumerated Simple Perfect Squared Squares (SPSSs) and Simple Imperfect Squared Squares (SISSs) with 30 squares (order 30). In January/February James Williams found large numbers (over 15 million) SPSSs in orders from 30 to 44. It is now possible to extend the listing of optimal Mrs Perkins's quilts even further. Here are some results for quilts with 30 squares;

In July-September 2013 Lorenz Milla and Stuart Anderson enumerated Simple Perfect Squared Squares (SPSSs), Compound Perfect Squared Squares (CPSSs) and Simple Imperfect Squared Squares (SISSs) with 31 and 32 squares (order 31,32). Here are some results for quilts with 31 and 32 squares;

Best Known, Not Best Possible

It needs to be stressed that most of the results here are the best known optimal quilts A089046, the majority of them (those past order 18) have not been proven to be the best possible. The rest of the optimals should be considered as conjectures. Conway stated [11]; "G.B.Trustrum and I proved that the answer lies between two constant multiples of log n." [1] [2]

Planar graphs can be used as electrical networks to create square tilings ie, squared rectangles and squared squares. To create quilts, 2-connected planar graph embeddings need to be used, in addition to the 3-connected graphs. These 2-connected graphs are far more numerous than the 3-connected graphs. This limits what is possible using this method. With the large number of graphs, fewer orders can be exhaustively searched. In addition many quilts can only be modelled with planar multi-graphs. A multi-edge represents a contiguous block of same size squares. Multi-edge graphs are even more numerous than the simple 2-connected graphs. Plantri, the graph generator used to produce 2 and 3 connected graphs, only produces simple graphs. However it should be possible to simulate multi-graphs using plantri simple graphs with resistances of n and 1/n for n multi edges between 2 vertices, in a similar manner to Jepsen and Gu's [8] work on rectangles dissected into rectangles, then dissect the rectangles so they become the blocks of same size squares. It may be possible to prove several more orders as best possible using this method.

Recent work by Ed Wynn, and updated OEIS Sequences

A recent (August 2013) paper by Ed Wynn[14] extends the exhaustive generation of all squared square dissections, having relatively prime sides (Mrs Perkins's quilts) up to order 18, using the plantri software with a graph theoretical approach which is different to the electrical network method of BSST/Duijvestijn. The results were cross-checked by generating all dissections of small sizes using Knuth's dancing links algorithm to produce exact cover square dissections. In the paper's appendix, Ed lists values from several sequences in the OEIS with previously known values that have been confirmed in the current work (or, conversely, have been used to check the current work). Also, new (or newly definite) values are shown in italics.

These sequences include the trivial dissection of a square into itself (except where ‘smaller’ is specified, in A018835 and A211302). Sequences A045846 and A221845 have known values beyond those listed here. In particular, A045846 is known for n ≤ 15 – and the values for 10, 11 and 12 (1500957422222, 790347882174804 and 781621363452405930) were used to confirm and extend A224239.

Conjectured OEIS terms for optimal quilts and largest quilts of a given order

Sequence A089046 ; "Least edge-length of a square dissectable into at least n squares in the Mrs Perkins's quilt problem.", lists the optimal quilts as the lowest known size for a given square of order n. It is possible to conjecture additional terms to this sequence and the following one, based on incomplete squared square enumeration, beyond what has been proved by Wynn (conjectured terms are in bold).
1, 2, 2, 2, 3, 3, 4, 5, 6, 8, 10, 14, 18, 24, 30, 40, 54, 71, 92, 121, 155, 210, 266, 360, 476, 642, 833, 1117, 1485, 1967, 2595, 3465, 4534,

Sequence A089047 ; "Greatest edge-length of a square dissectable into up to n squares in the Mrs Perkins’s quilt problem.", lists the quilts with the greatest known size for a given square of order n. (conjectured terms are in bold).
1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 13, 17, 23, 29, 41, 53, 70, 91, 126, 158, 216, 276, 386, 488, 675, 866, 1179, 1544, 2136, 2739, 3755, 4988, 5976, 6443

Mrs. Perkins’s Quilt Update July 2017.

by Ed Pegg Jr

I’ve updated the results for demonstrations.wolfram.com/MrsPerkinssQuilts/ to 40000. As a result, many of the results at squaring.net/quilts/mrs-perkins-quilts, A089046, and A089047 can be extended.

Current A089046: 1, 2, 2, 2, 3, 3, 4, 5, 6, 8, 10, 14, 18, 24, 30, 40, 54, 71, 92, 121, 155, 210, 266, 360, 476, 642, 833, 1117, 1473, 1967, 2595, 3465, 4534,

Current with improved conjectured extra terms (emphasised) A089046: 1, 2, 2, 2, 3, 3, 4, 5, 6, 8, 10, 14, 18, 24, 30, 40, 54, 71, 92, 121, 155, 210, 266, 360, 476, 642, 833, 1117, 1485, 1967, 2595, 3465, 4534, 5995, 7907, 10293, 13505, 17785, 23239, 31035, 39571

Here are builds for the ten ending values for A089046. Each of these has many solutions. The ten primitive quilts used to build the squares follow afterwards.

builds for the ten ending extended values for A089046

Mrs Perkins's Quilts builds for the ten ending (extended) values for A089046

Current A089047: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 13, 17, 23, 29, 41, 53, 70, 91, 126, 158, 216, 276, 386, 488, 675, 866, 1179, 1544, 2136, 2739, 3755, 4988, 5976, 6443

Current with improved conjectured extra terms (emphasised) A089047: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 13, 17, 23, 29, 41, 53, 70, 91, 126, 158, 216, 276, 386, 488, 675, 866, 1179, 1544, 2136, 2739, 3755, 4988, 6443, 8568, 11357, 14877, 19594 , 26697, 34632,...

Here are builds for the eight ending values for A089047. Most of these have unique solutions. The primitive quilts used to build the squares follow afterwards.

builds for the eight ending extended values for A089047

Mrs Perkins's Quilts builds for the eight ending (extended) values for A089047

The procedure for this update was

  1. http://www.squaring.net/downloads/downloads.html#pss -- Downloaded all squares.
  2. http://www.squaring.net/sq/ss/siss/siss.html -- Downloaded all squares, then stripped away the 16 build methods I've identified. From the above, I obtain a list of Prime quilts that are not a simple derivation of a smaller square quilt and which have a potential to be used for an optimal quilt. I seem to have a list of 64902029 prime quilts.
  3. Given: number of squares, side of quilt, and size of corners of an existing quilt. A fast routine exists for determining the 16 builds that are aimed at each of the 4 corners. So 64 possible builds for each quilt at each build step.
  4. For each of the 64902029 prime quilts, do an order 7 recursion (64^7 =4398046511104 possible) and pick out any new records.
  5. Keep track of how each record got built. Many records had unique build methods. When a prime quilt could set records, it was usually useful for building many other quilts. In my final build, I had 3656 prime quilts that could build all quilts up to size 40000. Every single list of squares from squaring.net yielded new records by the time I finished processing it. Thus, the records are a bit fragile.

All of the SPSS and SISS solutions at squaring.net are based on polyhedral graphs with a given number of edges, http://oeis.org/A002840 .

However, from the SISS solutions, it's possible to strip away the outer shell to obtain a prime quilt that is based on a 2-connected graph instead of a 3-connected graph. These 2-connected solutions tend to be floppy with many ways to arrange the squares. Usually, that means the 2-connected sub-element can be moved to a corner, and the "defect" removed to make a 3-connected version, which is then found in the SISS search. My list of prime quilts has many 2-connected quilts. The SISS-32 list gave a handful of new records for orders 28-30.

The attached list is likely very reliable up to order 33. When complete solutions for SPSS and SISS up to order 37 are known, probably 10 or so of the solutions up to size 10000 will need to be corrected, if the huge search detailed above is done.

Denote the order of the minimal squares in a Mrs. Perkins’s Quilt of size s as mpq(s). Some plots follow;

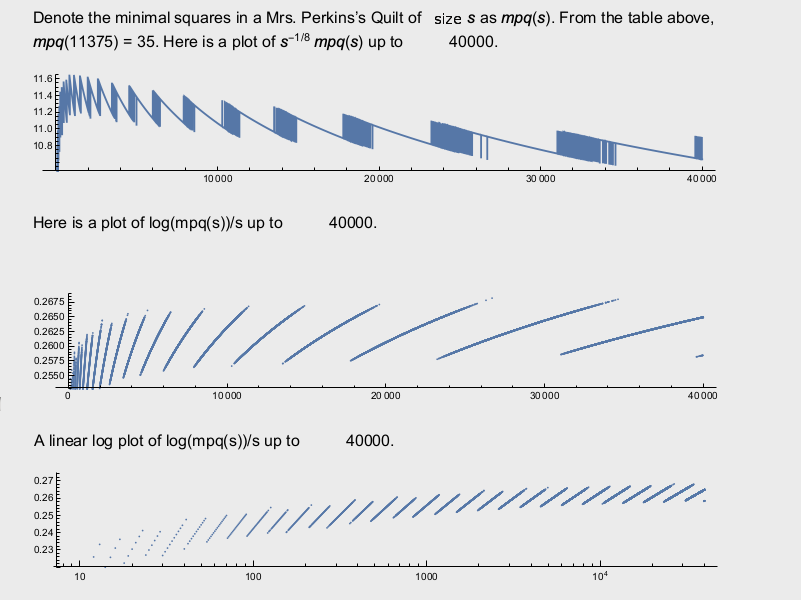
Plots of minimal squares in a Mrs Perkins's Quilt of order s

Plots of minimal squares in a Mrs Perkins's Quilt of order s

Part of the current table of best known solutions for order 6 and up.

Optimal Mrs Perkins's Quilts

A list of 40000 currently best known quilts, from size 1 to 40000, is here (2.7M). A zipped postscript file (3.1M) of those quilts is here. There are sometimes many quilts with the same size and order, only one representative was chosen. These quilts are a combination of Ed Pegg's optimal listings and the optimal quilts from this site, they are only 'optimal' with respect to the the best known results, and in some cases the best possible for low orders (<= order 18) and small sizes, up to order 40.

    References;
  1. Dudeney, Henry Ernest. "Mrs. Perkins's Quilt.", Amusements in Mathematics, 1917. (Project Gutenberg)
  2. Conway, J. H. "Mrs. Perkins's Quilt." Proc. Cambridge Phil. Soc. 60, 363-368, 1964.
  3. Trustrum, G. B. "Mrs. Perkins's Quilt." Proc. Cambridge Phil. Soc. 61, 7-11, 1965
  4. M. Gardner, "Mrs. Perkins's Quilt and Other Square-Packing Problems," Mathematical Carnival, New York: Vintage, 1977.
  5. H. T. Croft, K. J. Falconer, and R. K. Guy, Section C3 in Unsolved Problems in Geometry, New York: Springer, 1991.
  6. Conway, J. H. "Re: [math-fun] Mrs. Perkins's Quilt - Orders 89, 90 improved over UPIG." math-fun@mailman.xmission.com mailing list. October 10, 2003.
  7. Ed Pegg, Jr., Square Packing and Mrs Perkins's Quilts
  8. Ed Pegg, Jr., Demonstration Wolfram Mrs Perkins's Quilts
  9. Weisstein, Eric W. "Mrs. Perkins's Quilt." From Mathworld--A Wolfram Web Resource http://mathworld.wolfram.com/MrsPerkinssQuilt.html
  10. Charles H. Jepsen*, Ming Gu. "Dissections of p : q rectangles into thirteen p : q rectangular elements". Department of Mathematics, Grinnell College , 2004
  11. Paul J. Nahin "Mrs. Perkins's Electric Quilt: And Other Intriguing Stories of Mathematical Physics"
  12. R. K. Guy, OEIS A089046, "Least edge-length of a square dissectable into at least n squares in the Mrs Perkins's quilt problem."
  13. Antreas P. Hatzipolakis and J. H. Conway Math Forum Discussions
  14. Ed Pegg Jr, Lance Gay, Erich Friedman, Richard Guy, Bouwkamp, Duijvestijn and Antony Boucher, optimal quilt listings, primitive quilts, C programs
  15. Ed Wynn. Exhaustive generation of ‘Mrs Perkins’s quilt’ square dissections for low orders.