Order 26 Compound Perfect Squared Squares (CPSSs)
There are 16 CPSSs in order 26. These CPSSs were found by a variety of people over a period stretching from 1940 to 2010.
- tablecode (16) CPSS; Order 26 cpsso26.txt
- boukampcode (16) CPSS; Order 26 cpsso26.bkp
- (16) CPSS; Order 26
 cpsso26.pdf
cpsso26.pdf
- (100) CPSS isomers ; Order 26
 cpsso26-isomers.pdf
cpsso26-isomers.pdf
1940 R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T.Tutte published 'The Dissection of Rectangles into Squares", referring to an empirically constructed order 26 CPSS, side 608, attributed to Tutte. This is one of 16 isomers.
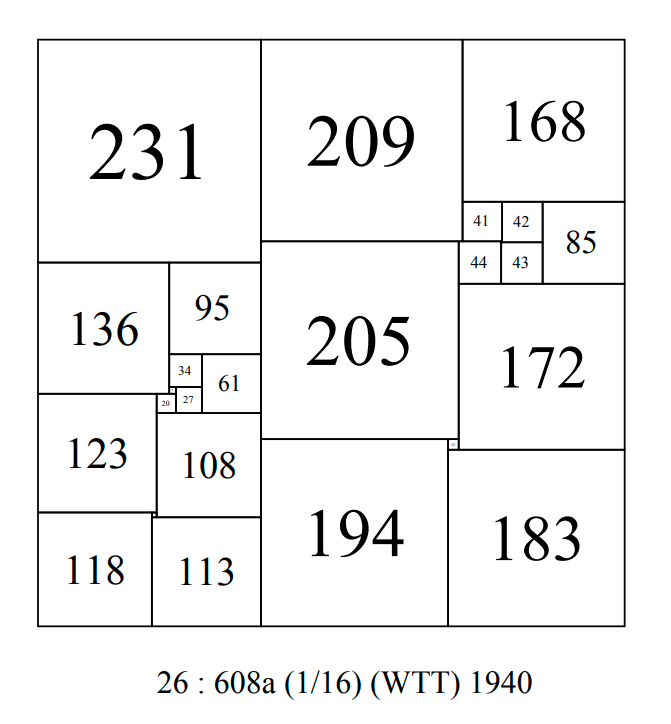
Order 26 : 608a (16) WTT 1940.
In 1951 T.H.Willcocks, published 'A note on some perfect squared squares', his account of the methods he used to construct CPSSs with small sizes. He included a number of new squared squares, these included his discovery of a new CPSS of order 26 with side 492, and 2 new CPSSs of order 27 with sides 872 and 890.
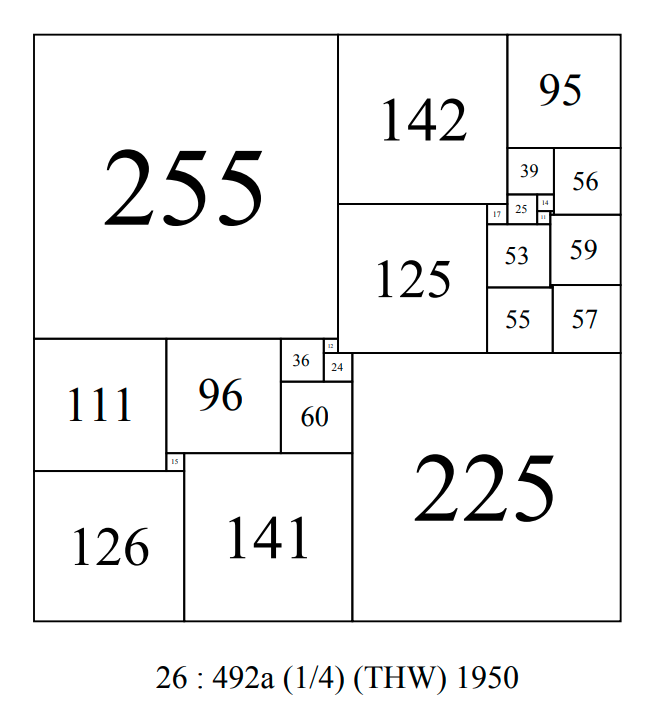
Order 26 : 492a (16) THW 1950.
In 1964 a detailed account of some low-order perfect squared square construction methods was given by P. J. Federico in a paper 'A note on some low-order perfect squared squares' . One of the most productive methods was Method 8. Squared hexagons with two opposite sides equal.
Federico used this method to produce 17 out of the 35 low-order simple perfect squared squares listed in his paper, including this order 26 CPSS with side 384, with a subrectangle 99x205, split to a 99 square and an order 12 99x106 SPSR.
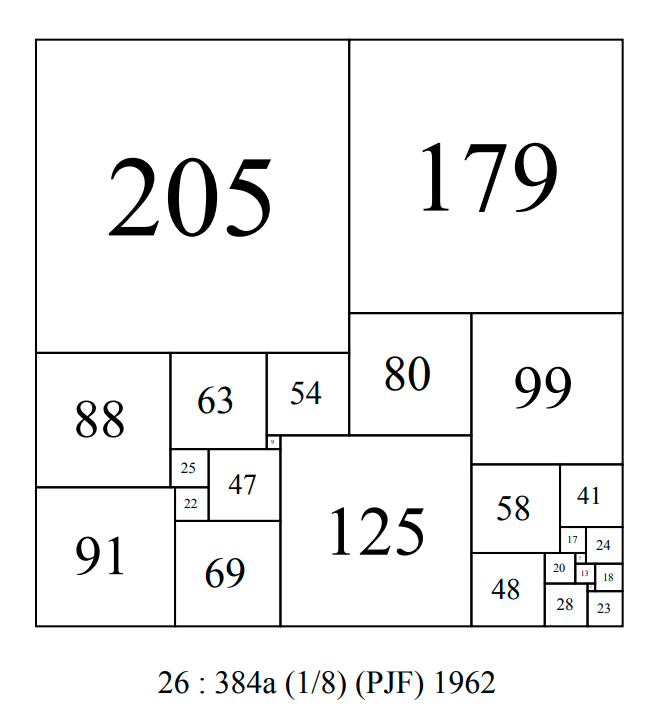
CPSS Order 26 : 384a PJF 1964
In 1964 P. J. Federico published a CPSS with side 429 of order 26 using a type of Fibonacci sequence construction published by S. Basin in 1963.
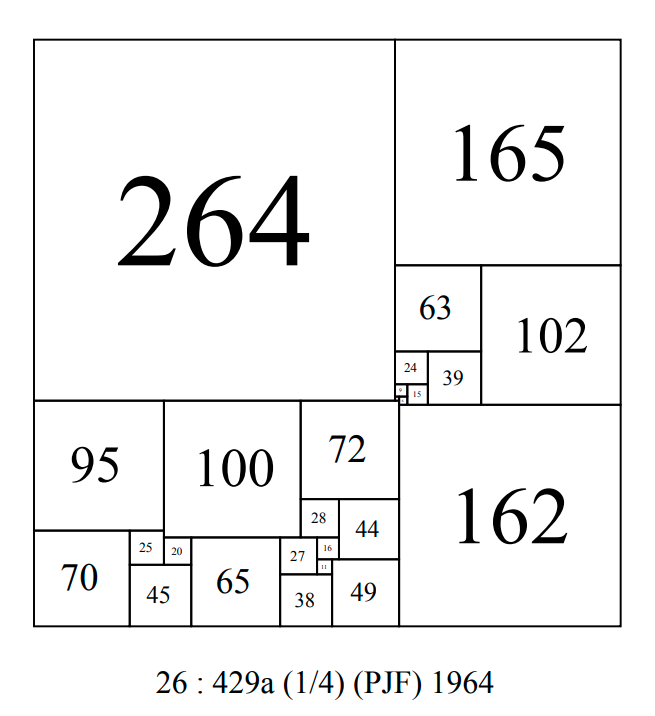
CPSS order 26 : 429a PJF 1964, using a Fibonacci sequence construction.
In 1965-69 E. Lainez, a Spanish engineer, constructed 2 CPSSs with sides 360, 460 of orders 26 and 27 respectively.
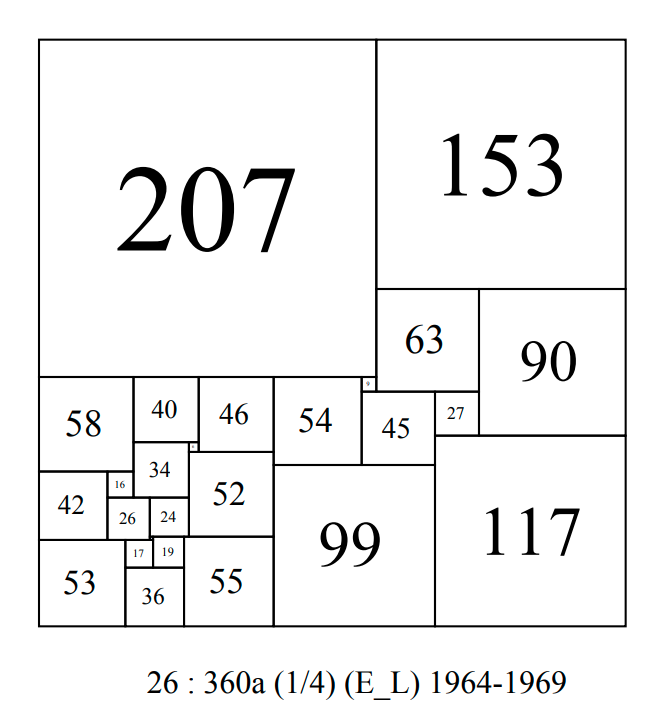
CPSS order 26 : 360a E_L.
Over the rest of 1960's and into the early 1970's, a number of further order 26 CPSS discoveries were made by Bouwkamp and Federico. Exact dates of discovery are not known.
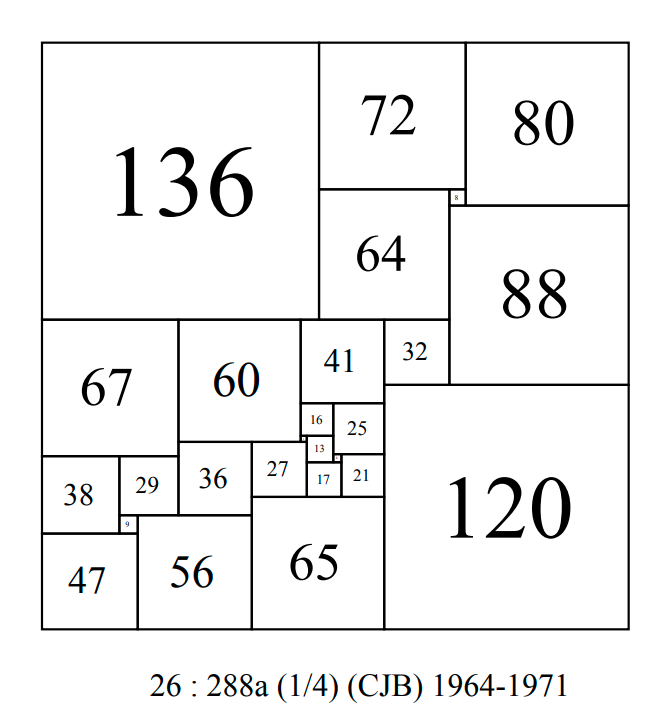
CPSS order 26 : 288a-CJB
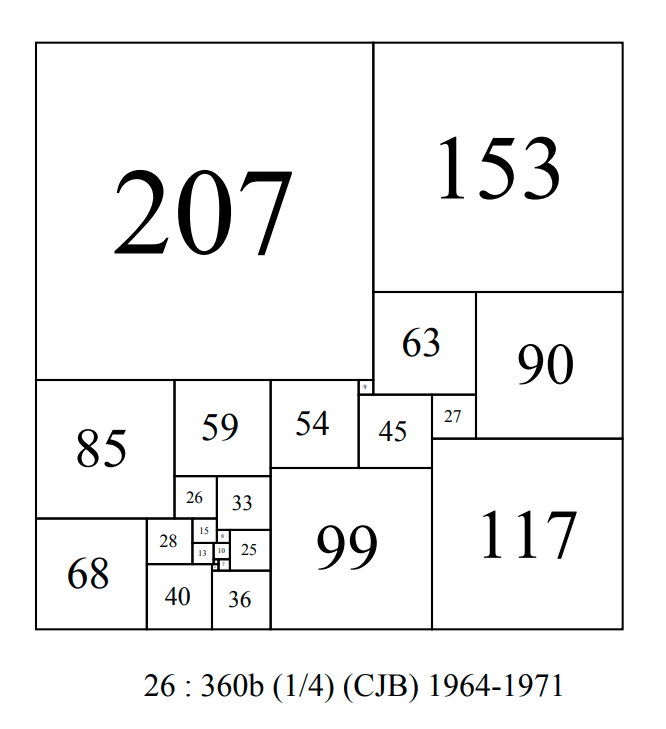
CPSS order 26 : 360b-CJB

CPSS order 26 : 429a-PJF
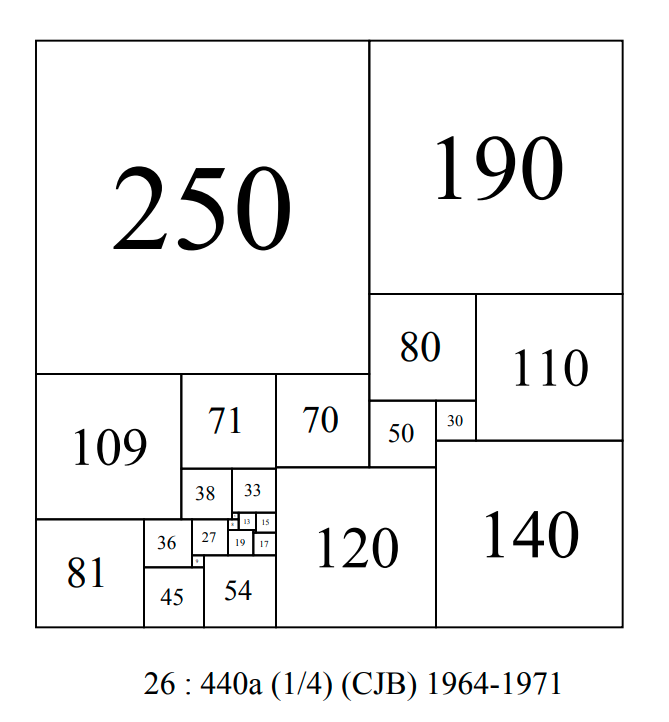
CPSS order 26 : 440a-CJB
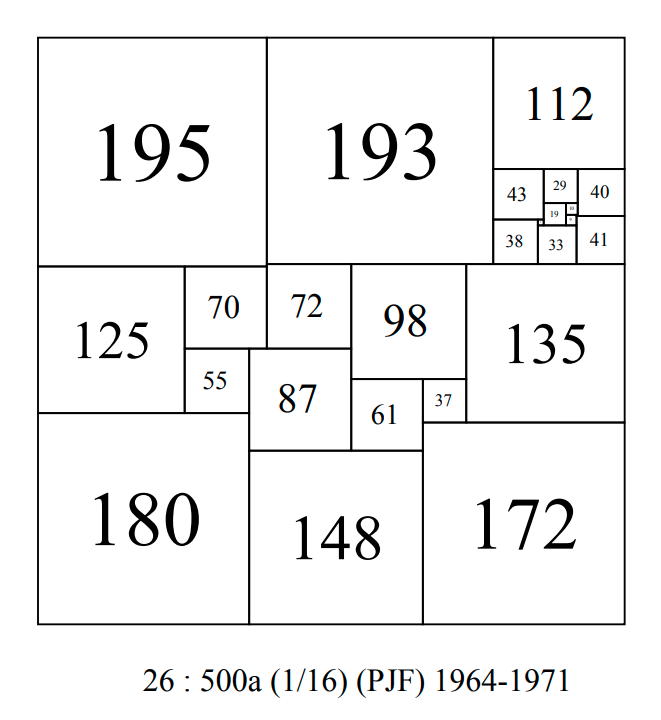
CPSS order 26 : 500a-PJF
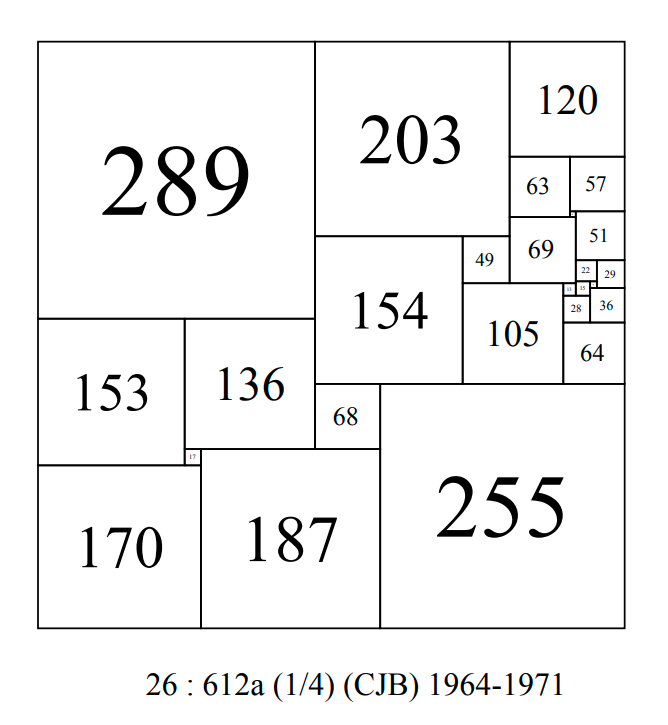
CPSS order 26 : 612a-CJB
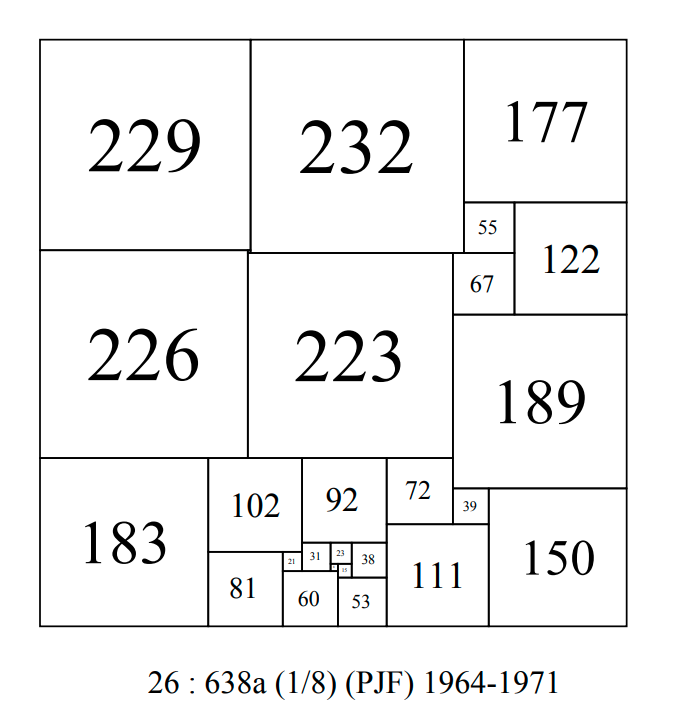
CPSS order 26 : 638a-PJF
Federico, Leeuw and Duijvestijn published a paper 'Compound Perfect Squares' in 'The American Mathematical Monthly Vol. 89, No. 1 (Jan., 1982), pp. 15-32' . The paper illustrated a CPSS of side 483 found during the research.
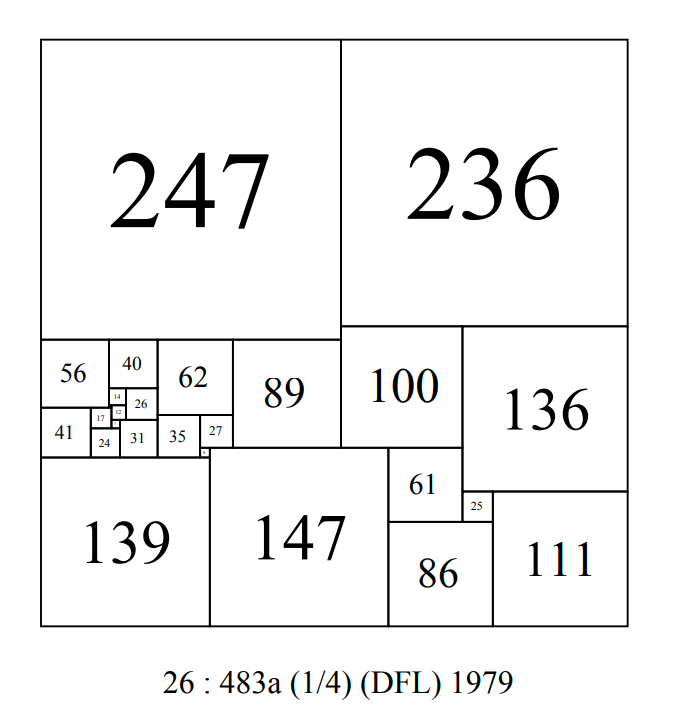
CPSS order 26 : 483a-DFL
Jasper Skinner became active in researching and constructing squared squares in the 1990's. He applied the known methods and discovered 3 new CPSSs of order 26.
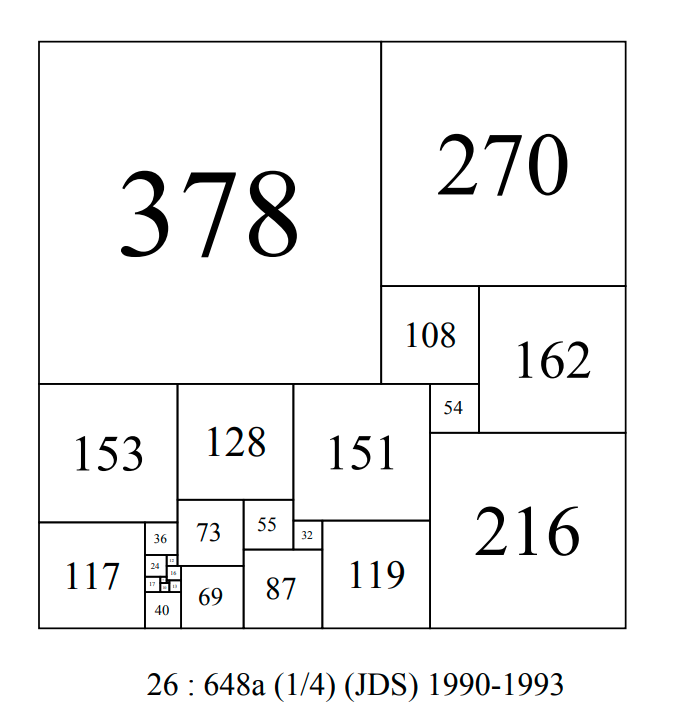
CPSS order 26 : 648a-JDS
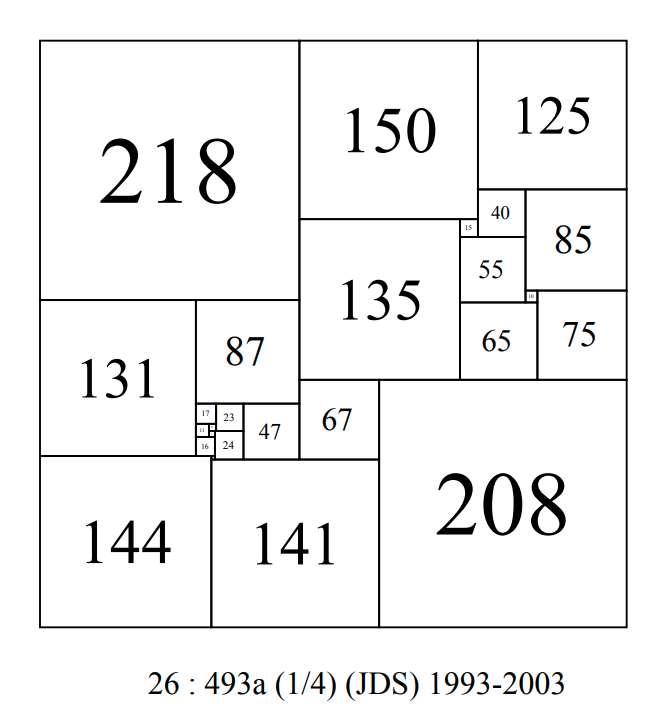
CPSS order 26 : 493a-JDS
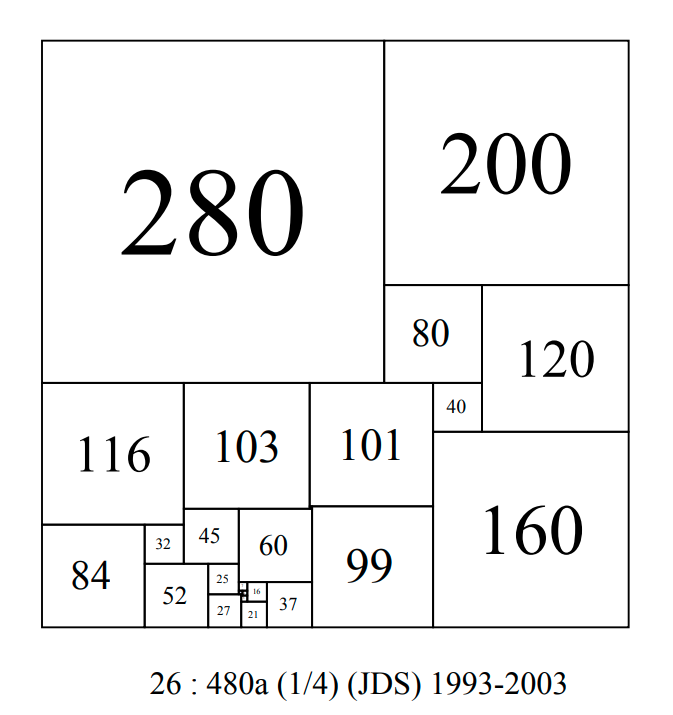
CPSS order 26 : 480a-JDS
In 1999 I. Gambini published his doctoral thesis 'Quant aux carrés carrelés' on squared squares. He found the known CPSSs (and SPSS) up to and including order 26. He also published a table of CPSR ( and SPSR) counts up to and including order 24. For order 26 he identified 100 CPSS isomers while only 92 isomers were known before Gambini's work. The additional square which completes the order (with side 512) has 8 isomers and was probably found by Paul Leeuw in 1979, as DFL report in the paper that they constructed over 2000 CPSS although only one other CPSS, 483a, from order 26 was published in the paper. Gambini did not mention the 512 order 26 CPSS in his thesis. This CPSS was evidently 'rediscovered' in 2010 by Anderson and Pegg, when it appeared in bouwkampcode/tablecode and as an image for the first time.
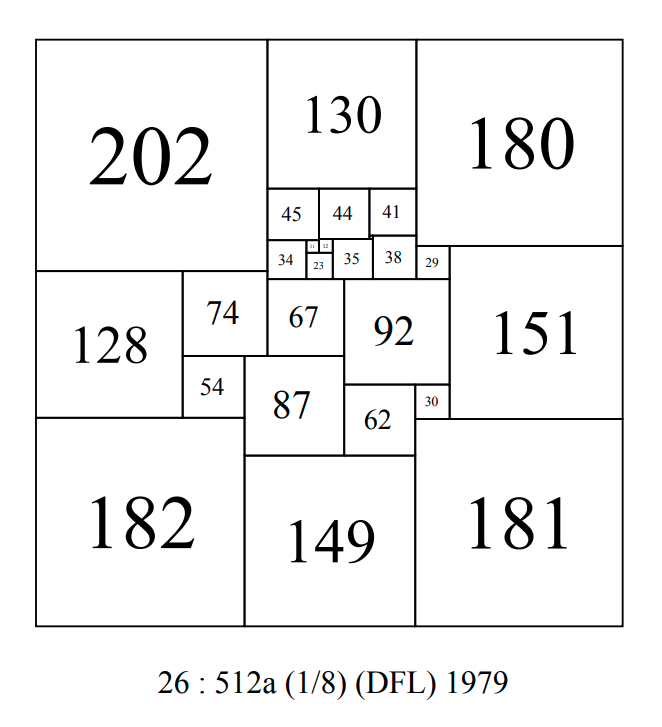
CPSS order 26 : 512a-DFL