Zbigniew Moroń(1904-1971), Wraclow, Poland
In 1925 Zbigniew Moroń published a paper, 'O Rozkladach Prostokatow Na Kwadraty' (On the Dissection of a Rectangle into Squares)[1].
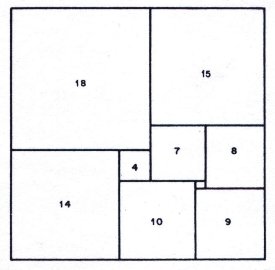
Rectangle I 33x32
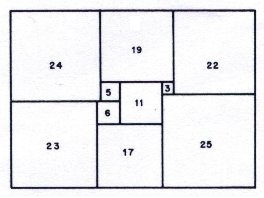
Rectangle II 65x47
Moroń gave the first examples of rectangles divided into unequal squares in his paper. He doesn't indicate how they were obtained.
Rectangle I is 33 x 32 in size and is divided into 9 unequal squares. Rectangle II is 65 x 47 and has ten squares.
According to correspondence quoted by P J Federico, [2] Prof Wladyslaw Orlicz wrote of Moroń in a letter to Dr. Stanislaw Dobrzycki of Lubin, Poland;
“Zbigniew Moroń was my younger schoolmate when studying mathematics at the University of Lwoów; about 1923-24 we were both junior assistants in the Institute of Mathematics. Professor Stanislaw Ruziewicz (who was then professor of mathematics at the University) communicated to us the problem of the dissection of a rectangle into squares. He had heard of it from the mathematicians of the University of Crakow who took interest in it. As young men we enthusiastically engaged ourselves in investigating this problem, but after some time we all came to the conclusion that it was certainly as difficult as many other apparently simple questions in number theory. The examples found by Moroń were to us a great surprise. Before the World War II Moroń was a teacher in secondary schools; after it he was too, and dwelt in Wraclow, where he died some 5 years ago.”
Further, in a translation of a later paper by Zbigniew Moroń, by Dr Dobrzycki, Zbigniew Moroń states,
"In the years 1925-28 I found further results in this domain; among others I proved that it is impossible to construct a rectangle with less than 9 different squares; I also knew of the dissection of a square which was later given by Sprague. Never-the-less I did not publish them, but only exposed them at meetings of the mathematical seminar of Professor Ruziewicz."
It is possible that Zbigniew Moroń discovered Sprague's square more than 10 years before Sprague himself, as the Sprague square is partly composed of the MorońRectangles I and II, but no other evidence has emerged to support the claim.
Federico noted Moroń introduced two conventions followed today,
- expressing sides of elements in integers (common factors removed) and
- writing the elemental side within the element.
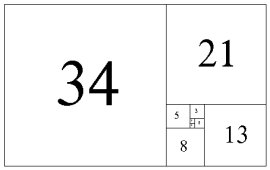
Golden Rectangle, Fibonacci sequence
Moroń noted that by adding a square of the same length of side to either side, the rectangle can be enlarged indefinitely.
Federico later recognised that continuing this process with alternate sides, the squares correspond to the Fibonacci sequence and therefore the ratio of sides in this infinite sequence approaches phi, the golden mean.
Starting with a 1x1 square this gives the famous golden rectangle, an imperfect squared rectangle.
Moroń's Squared Square Construction
Moroń raised the question “For what squares is it possible to dissect them into squares?”
He then observes “if there exists a rectangle (of different sides) for which there are two dissections R1 and R2 such that;
- in neither of these dissections does there appear a square equal to to the smaller side of the rectangle and,
- each square of dissection R1 is different from each square in dissection R2, then the square is dissected into squares, all different, as shown in the following figure.”
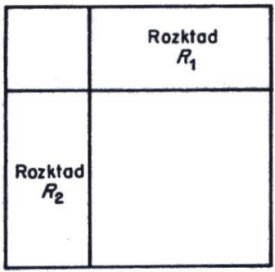
Moroń's figure
Moroń's (Un)solved Questions
"Moroń has asked if, in a squared rectangle there are always at least 2 squares that are surrounded by (four) larger ones. Also if, in a squared rectangle whose sides are relatively prime there is always a square that is a perfect square. Probably not. And is there a rectangle that can be squared in two distinct ways with no square ocurring in both squarings? Probably so."[4]
Moroń obviously formed his questions based on the two perfect rectangles he had knowledge of. Brooks, Smith, Stone Tutte read the Moroń papers and constructed many squared rectangles, also Michio Abe who read the Moroń papers had a 600 plus squared rectangle catalog. Inspection of the catalogue answers all of Moroń's questions.
For the first question if Moroń had known of the second order 9 perfect rectangle 61 x 69 he would have seen that when the smallest element and the second smallest element are adjacent it is possible for a tiling to be constructed where only the smallest element is surrounded by four larger squares.
Neither the smallest element or the second smallest element can be on the perimeter of the squared rectangle, a corner element must be larger than at least one of it's adjacents to avoid the adjacent squares overlapping, and these two elements are smaller than the others, they also cannot appear on the sides as no tile can be placed on their inner edge, the other elements are too big to fit, if we use the same tile twice the tiling is no longer perfect, and as they cannot appear in its corners, therefore they are surrounded on four sides. If these two elements are not adjacent, then both are always surrounded by four larger elements (they are the smallest elements, so the surrounding elements must be larger).
In his second question, Moroń conflates relatively prime sides with perfect square elements (A perfect square in this context meaning a square number 1, 4, 9, 16, 25 ...). If Moroń had known of order 10: 130 x 79, (10 130 79 45 44 41 3 38 12 35 34 11 23), he would find a perfect squared rectangle with relatively prime sides and no perfect squares among the elements. There are also perfect squared rectangles with sides having GCD > 1 and no perfect squares among the elements. The first example is order 13: 274 x 256, (13 274 256 147 127 20 48 59 109 58 37 11 70 51 7 44)
Following Moroń's interests in relatively primes sides and perfect squares, we can with our catalogues examine the data to find out how relatively primes sides and perfect squares are distributed among squared rectangles;
- what is the percentage of squared rectangles which have relatively prime sides?
- The data shows the percentage of relatively prime sided simple perfect squared rectangles drops from 100% at order 9 down to 89% by order 17.
- How many perfect square numbers (and what percentage of all squares) have been found in simple perfect squared rectangles (by order) ?
- The highest percentage of perfect square elements in a simple perfect squared rectangle which I've found so far is; 44.44% = 4 squares out of 9 elements; 69 x 61 (9 69 61 36 33 5 28 25 9 2 7 16) but close is 43.75% = 7 squares out of 16 elements; 169 x 119 (16 0169 0119 68 46 55 37 9 64 26 27 15 16 36 25 1 24 4 20).
Moroń's third question was solved by Brooks, Smith, Stone and Tutte [5] in two ways.
Firstly their rotor-stator network symmetry technique produced such distinctly squared rectangles. These rectangles were used in the Moroń construction as R1 and R2 to create order 69 and order 39 compound perfect squared squares.
Secondly Brooks, Smith, Stone and Tutte also kept adding to their collection of squared rectangles. As the squared rectangle catalogues grew examples of multiple rectangle dissections also appeared.
The smallest example of a rectangle that can be squared in two distinct ways with no square occuring in both squarings appears in order 13: 593 x 422. Arthur Stone created an order 28: 1015 compound perfect squared square (CPSS) using the Moroń construction with these two rectangles.
References
- 'O Rozkladach Prostokatow Na Kwadraty' (On the Dissection of a Rectangle into Squares) by Zbigniew Moroń, Prezeglad Mat. Fiz. 3 152-153 (1925)
- 'Squared Squares, Who's Who & What's What', p9 Jasper Dale Skinner, II, Ph.D. 1993
- A. Schonflies and M. Dehn, Ungeloste Probleme der analytischen Geometrie, in "Einfuhrung der analytischen Geometrie der Ebene und des Raumes', 2nd ed, Appendix VI, pp 402-411. Springer-Verlag. Berlin, 1931.
- Kenneth J. Falconer, Richard K. Guy, Hallard T. Croft, pp 81-82 in "Unsolved Problems in Geometry", 2nd ed, C2, 1991. ;
- 'The Dissection of Rectangles into Squares' by R.L. Brooks, C.A.B. Smith, A.H. Stone, and W.T. Tutte in Duke Mathematical Journal, vol. 7, pages 312-40, 1940.