T.H. Willcocks (1912 - 2014)
At WWII end, an able young Englishman became aware of and interested in the problem of squaring the square. This man was Theophilus Harding Willcocks (THW), also known as Theo (or Phil) Willcocks..

Theophilus Harding Willcocks (THW)
This talented amateur mathematician (and chess enthusiast) was born April 19, 1912, at Newquay, Cornwall, England. A modest man, THW was for many years, an employee at the Bank of England until his retirement. Since 1945, his continuing interest in the field was evidenced by his many outstanding productive contributions to its growing body of knowledge. His early publications appeared in the Fairy Chess Review (no longer published, but also see the website mayhematics by George Jelliss - mainly concerned with the history of work published in Fairy Chess Review). The Fairy Chess Review, along with his publications in the Canadian Journal of Mathematics [3] and the Journal of Combinatorial Theory [4] have demonstrated his unique approach to mathematical problems. THW discovered (in 1946) and subsequently published [2], a compound perfect squared square with 24 squares, which was for more than 30 years, prior to Duijvestijn's discovery of 21:112A, the most widely known perfect squared square. It was constructed by overlapping two squared rectangles, one perfect and the other containing a single trivial imperfection involving a corner square.
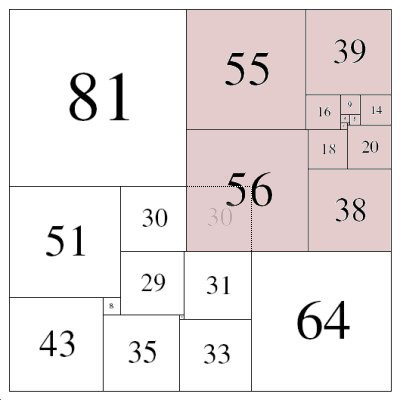
24 : 175 (THW) 1948, showing the overlapping rectangle construction
So many authors have cited this square that its figure is well known even to casual readers (with a broad spectrum of interests in mathematics, but unlikely to read the technical papers on the subject). "This little gem of Willcocks", as it has been called is 24: 175a (THW). For more than three decades, it was the benchmark by which all other squares were measured (as it had the lowest order and smallest side of any known perfect square) and it remains today, the lowest possible order compound perfect square, a fact established by Duijvestijn, P. J. Federico and P. Leeuw in 1982 [8]. Even today with conclusive permanent records of the ultra-low-order squares established, only three people have produced a square which betters this square in size and order ... Willcocks is one of these (Duijvestijn and Skinner are the others), Willcocks found 22:110B by hand, by applying a transform to Duijvestijn's 22:110A. "In July of the same year (1978), Duijvestijn found two simple perfect squared squares of order 22 (22:110A and 22:192A). After communicating these to P.J. Federico of Washington, D.C., U.S.A., who informed T.H. Willcocks of Bristol, U.K., the latter found a third simple perfect squared square of order 22 about August 1978."[5]
We now know that there are 3 perfect squared squares with side 110. Twelve years after the first two were discovered, a third SPSS with 23 squares and a side of 110, 23:110A, was discovered by Duijvestijn in 1990 in a computer search. These 110 squares are the smallest side possible in a perfect squared square, a fact proved by Gambini in 1996 [9]. All the ultra-low-order squares (from order 21 through 24) are now known [5]. All but one of these are simple. 24:175a (THW) is compound. It stands alone.
Theo Willcocks produced many squared squares over more than half a century, inventing new techniques and methods on a regular basis [6]. Working alone and in collaboration with Federico and others, he was able to equal or better many of the results produced by brute force computer enumeration.
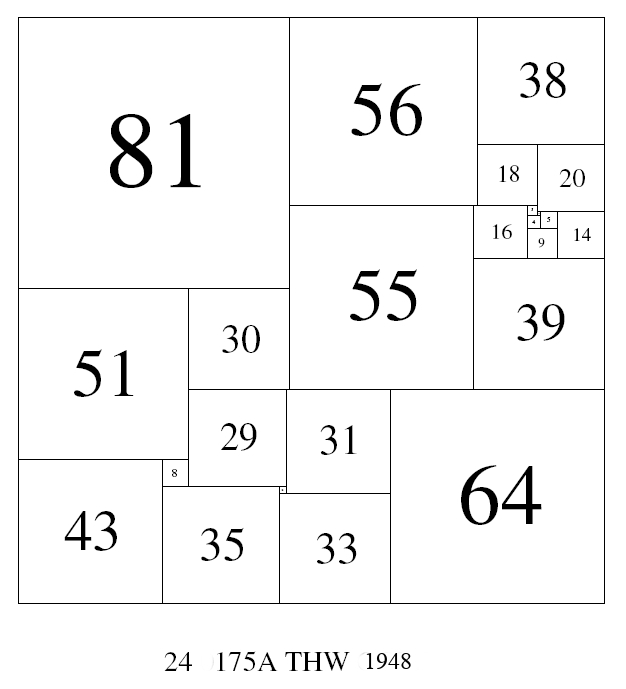
24 : 175 (THW) discovered 1946, published 1948
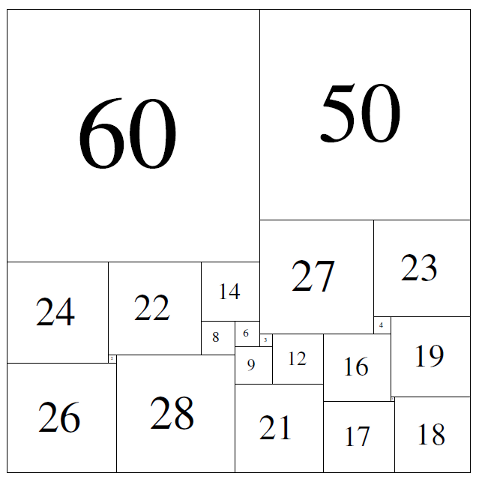
22 : 110B (THW) discovered 1978 (1 of 3 smallest PSS)
In recent correspondence George Jelliss stated; "I’ve never actually met THW in person, but he was a member of the Fairy Chess Correspondence Circle (made up of contributors to Fairy Chess Review) when I was invited to join it in the 1970s. One of his interests was in retroanalytical “last-move” compositions. These chess problems all take the form of asking “what was the last move”. The Schwalbe chess problem database contains 34 last move problems by Theophilus Harding Willcocks [7]. To see all of them, go to The Schwalbe Chess Problem Database and search with A='Willcocks'.
George Jelliss; "He and H. E. de Vasa were the first to construct diagonally magic knight’s tours on the 16x16 and larger boards (following on from the work of H. J. R. Murray who died in 1955). He published articles in Recreational Mathematics Magazine 1962 and Journal of Recreational Mathematics 1968 on this subject. Most of my correspondence with him was in connection with magic knight’s tours, and tours by other pieces. He also contributed a few cryptarithms to my Games and Puzzles Journal. One “composed to mark a young brother’s 70th birthday” is: THIRTY + TWENTY + TEN + SEVEN + THREE = SEVENTY."
Theo, short for Theophilus, like his father, worked all his career for the Bank of England, latterly on exchange controls. During the war he served in Italy and North Africa in the RAF.
Willcocks was one of three brothers. His youngest brother was Sir David Willcocks CBE MC (born 30 December 1919, died 17 September 2015) was a distinguished and well-known British choral conductor, organist, and composer. The three brothers remained close and in their twilight years worked together to restore the pipe organ in the beautiful Parish Church of St Michael at Newquay where they attended services with their parents throughout their childhood.
The second brother Wilfrid Willcocks was a Japanese POW in WWII and went on to live an interesting and productive life. He became a successful investment analyst. He wrote about market developments for the Financial Times, became a member of the Stock Exchange and a Lloyds name. In retirement he continued to play the stock market with success, outperforming it through booms and recessions. He established a trust which will continue to support environmental and social charities. Wilfrid died in 2011 aged 96.
T.H. Willcocks was 100 on April 19, 2012.
Phil died peacefully on 14th April five days before his 102nd birthday. The funeral was held at Cambridge Crematorium on Thursday April 24th.

Theo Willcocks - THW (left), Wilfrid Willcocks (centre),
David Willcocks (right)
The biographical sketch is based on contributions from Jasper Skinner, Geoffrey Morley and George Jelliss.
Bibliography
- Willcocks, T.H. Problem 7523 and solution, Fairy Chess Review 6 (1947-1948) p114 (Dec); p123 (Feb).
- Willcocks, T.H. Problem 7795 and solution, Fairy Chess Review 7 (1948) p97 (Aug); p106 (Oct)
- Willcocks, T.H. A note on some perfect squared squares. Can. J. Math. 3, p304-308 (1951).
- Willcocks, T.H. Some squared squares and rectangles. J. Comb. Theory 3, p54-56 (1967).
- C.J. Bouwkamp and A.J.W. Duijvestijn, Catalogue of Simple Perfect Squared Squares of orders 21 through 25, EUT Report 92-WSK-03 Eindhoven, (November 1992)
- Willcocks, T.H. Squaring the Square (28 May 2004) The Games and Puzzles Journal — Issue 35, September-October 2004
- The Schwalbe Chess Problem Database; search with A='Willcocks'
- A. J. W. Duijvestijn, P. J. Federico, and P. Leeuw, "Compound Perfect Squares", Amer. Math. Monthly 89 (1982) pp 15-32
- "Quant aux carrés carrelés"; Ian Gambini, THÈSE L’UNIVERSITÉ DE LA MÉDITERRANÉE AIX-MARSEILLE II, École doctorale de Mathématiques et Informatique, Décembre 1999
- Jasper Dale.Skinner II, Squared Squares, Who's Who and What's What.(1993)