Squared Möbius Strips
The Möbius strip or Möbius band (UK /ˈmɜrbiəs/ or US /ˈmoʊbiəs/; German: [ˈmøːbi̯ʊs]), also Mobius or Moebius, is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.
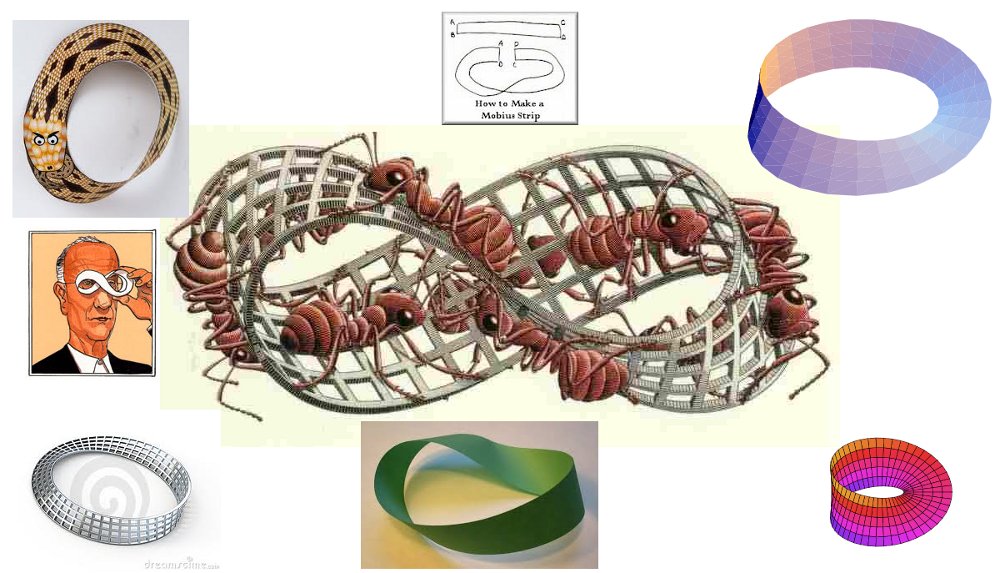
A variety of Möbius strips. The comic strip portrait is Jean Giraud aka Moebius (1938-2012), who created a wide range of science fiction
and fantasy comics in a highly imaginative and surreal, almost abstract style. The central image with ants is by Escher.
A model can easily be created by taking a paper strip and giving it a half-twist, and then joining the ends of the strip together to form a loop. In Euclidean space there are two types of Möbius strips depending on the direction of the half-twist: clockwise and counterclockwise. That is to say, it is a chiral object with "handedness" (right-handed or left-handed).
The Möbius band (equally known as the Möbius strip) is not a surface of only one geometry (i.e., of only one exact size and shape), such as the half-twisted paper strip depicted in the illustration below. Rather, mathematicians refer to the (closed) Möbius band as any surface that is homeomorphic to this strip. Its boundary is a simple closed curve, i.e., homeomorphic to a circle. This allows for a very wide variety of geometric versions of the Möbius band as surfaces each having a definite size and shape. For example, any closed rectangle with length L and width W can be glued to itself (by identifying one edge with the opposite edge after a reversal of orientation) to make a Möbius band. Some of these can be smoothly modeled in 3-dimensional space, and others cannot.
Topologically, the Möbius strip can be defined as the fundamental square [0,1] × [0,1] with its top and bottom sides identified by the relation (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1, as in the diagram on the right.
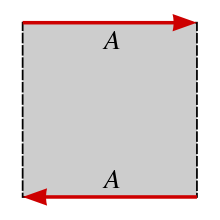
Gluing top & bottom edges of
a square to create a Möbius strip.
The Möbius strip is a compact nonorientable two-dimensional manifold (i.e. a surface) with boundary. It is a standard example of a surface which is not orientable. In fact, the Möbius strip is the epitome of the topological phenomenon of nonorientability. This is because 1) two-dimensional shapes (surfaces) are the lowest-dimensional shapes for which nonorientability is possible, and 2) the Möbius strip is the only surface that is topologically a subspace of every non-orientable surface. As a result, any surface is non-orientable if and only if it contains a Möbius band as a subspace.
We are interested in dissecting the surface of the fundamental polygon when it is a square, (or rectangle with the same gluing instructions), into a finite number of smaller squares, called the elements. As a Möbius strip has a boundary, the edges of the square elements of the dissection must be parallel with edges of the fundamental polygon.
The sizes of the elements are commensurate with each other and can be expressed as integers divided by any common factor. If the sizes of the elements dissecting a Möbius strip are all distinct, (no two the same size), then we call the dissection perfect. The number of elements in the dissection is called the order. We call a tiling faultfree if has no fault line, which is what we call a glued edge that does not intersect any tiles. We use the abbreviation FPSMB for Faultfree Perfect Squared Möbius Band, and NPSMB for Nonfaultfree Perfect Squared Möbius Band.
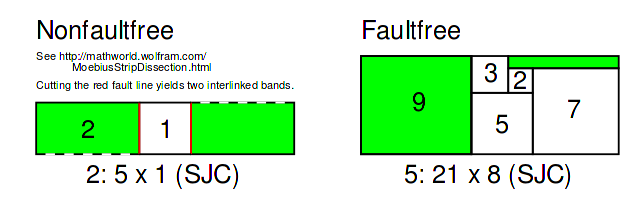
An order 2 (with fault) and order 5 (faultfree) squared Möbius strips
In 1991 Bracewell found a squaring of the Mobius strip using only 8 squares. In 1993 S.J. Chapman found that 1 x 5 Möbius strip can be tiled by 2 squares, to accomodate this, one must extend the notion of tiling to allow the mapping of the squares into the surface to self-intersect on their boundaries, that is it contains a fault line and is not faultfree. Chapman found there are no order 3 or 4 squarings of the Möbius strip but that there is a unique order 5 squaring.
Geoffrey Morley has found 3 FPSMBs of order 10. He conjectured that there are no other faultfree tilings with fewer than 11 squares, with the shorter edge given a half twist.
However in 2024 Lex Augusteijn notified that he had found another Möbius strip of order 10. It is 57x65 and dissected into squares of sizes 2,4,5,7,9,16,25,28,29,and 32.
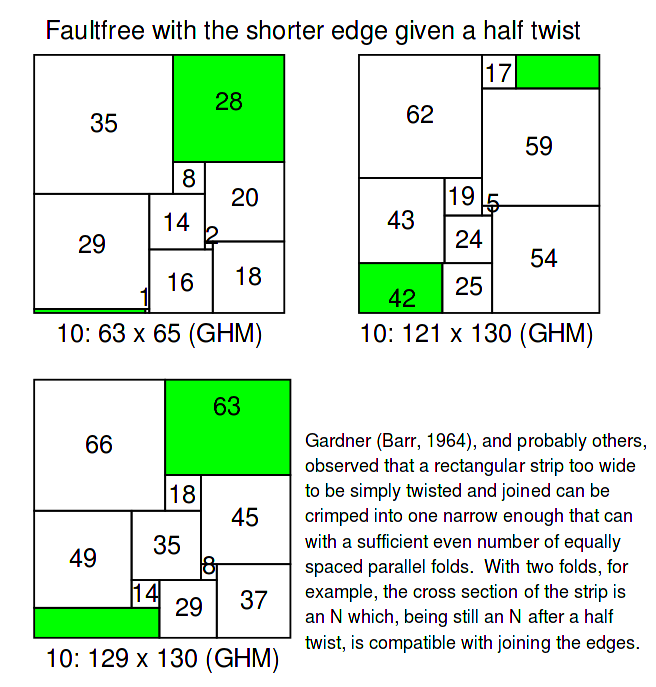
3 order 10 faultfree squared Möbius strips by Geoffrey Morley
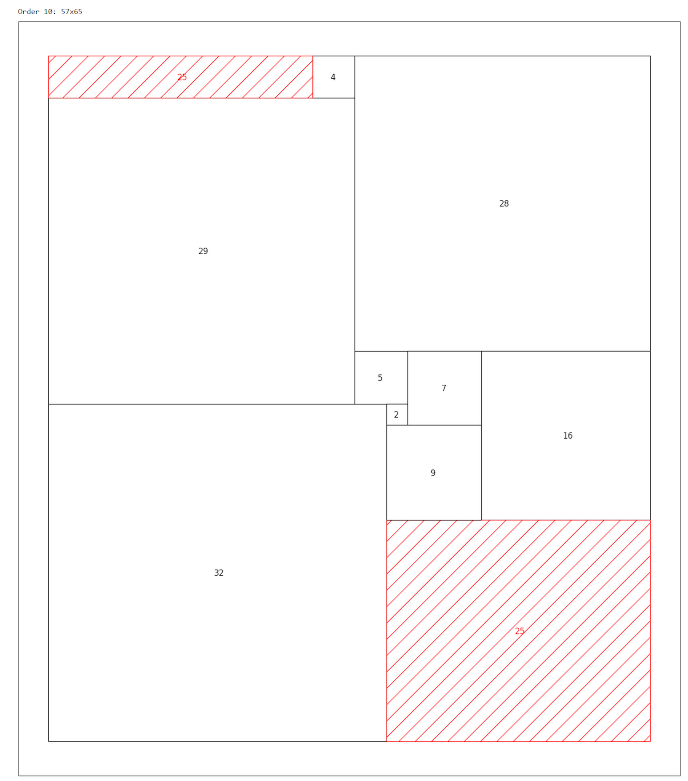
Order 10 57x65 faultfree squared Möbius strip by Lex Augusteijn