Simple Perfect Square-Cylinders (SPSCs);
Order 20
In the seminal paper "The Dissection of Rectangles into Squares" [1] by Brooks, Smith, Stone and Tutte, a number of generalisations of squared rectangle dissections were considered, including squared cylinders and tori, "10.2. Squared cylinders and tori. We may regard a squared rectangle, after identification of its left and right sides, as a "trivial" example of a squared cylinder. The squared cylinders are found to correspond exactly to the relaxation of the condition (1.12) that no circuit of the p-net may enclose a pole. A second step brings us to the "squared torus". Using the existence theorem of (9.45), we can easily construct such figures. It is also possible to construct a simple non-trivial perfect torus; but this is not so easy. Of course, the word "squared" may be replaced by "rectangled"."[1]
In 1983 Augusteijn and Duijvestijn published a paper, Simple Perfect Square-Cylinders of Low Order [2]. A Simple Perfect Square-Cylinder (SPSC) is a cylinder dissected into squares, all of different integer sizes, with no smaller dissected rectangle or square, where the height of the cylinder is equal to its circumference. Prior to Augusteijn and Duijvestijn the lowest order SPSCs known were of order 24, due to J. C. Wilson [3]. In [2], Augusteijn and Duijvestijn wrote; "We report the existence of two simple perfect square-cylinders of order 20 shown in Figs. 1 and 2. Dissected cylinders are associated with graphs which we call cyl-nets. A cyl-net is obtained from a dissected cylinder in the following way. The two rims of the cylinder are associated with two vertices which are called “source” and “sink,” respectively. Each horizontal line is associated with a vertex, while each square element is associated with an edge."[2]
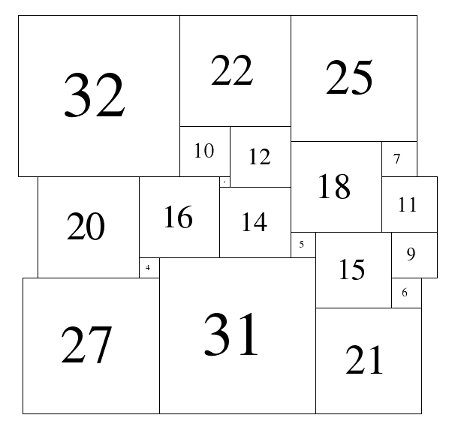
Figure 1; 79x79 Square-Cylinder A&D (1983)
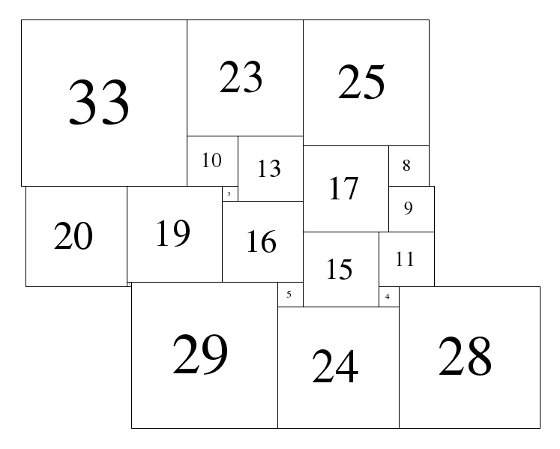
Figure 2; 81x81 Square-Cylinder A&D (1983)
"Since a dissected cylinder can be embedded on a sphere the associated cyl-net is planar. In case the cyl-net is 3-connected it must be a c-net. We are not interested in 1-connected graphs since they are associated with compound dissections; that is, two cylinders on top of each other. The class of 2-connected cyl-nets needs of course to be considered. This class can be constructed out of two cyl-nets of lower order."[2]
"Cyl-nets of orders up to and including 16 were generated and all possible dissections were calculated by means of a computer. We did not find a simple perfect square-cylinder of order 16 or lower. Of orders up to and including 20 only those cyl-nets were investigated that originated from c-nets of corresponding orders. Among those we found two simple perfect square-cylinders both of order 20."[2]
In 1993 S.J. Chapman [5] investigated the dissection of rectangles, cylinders, tori and Möbius strips. He found the 2 Simple Perfect Squared Rectangles (SPSRs) of order 9 (33x32 and 69x61), he also found that when the ends of the 33x32 rectangle are identified, it can be tiled in an additional way using the same squares creating a Simple Perfect Rectangle-Cylinder (SPRC). The same can be done with the 69x61 rectangle, and that these two SPRCs are of the smallest possible order. Chapman considered, but did not extend his methods to SPSCs as the number of matrices he would need to generate 'becomes prohibitively large'. [5]
- In 1999, in his thesis [6], Ian Gambini investigated squared rectangles, squared squares, squared tori and square cylinders, and in Chapter 6, published "interesting decompositions of square cylinders found by our algorithm"; (translation from French by Google Translate)
- 'the cylinder "square" of order and minimum size that we found'; [illustration of 79x79, of order 20]
- 'the cylinder "rectangular" minimum order found;' [illustration of 111 x 98, of order 10]
- 'the cylinder "rectangular" minimum size found;' [illustration of 56 x 52 , of order 16]
In 2012, Stuart Anderson and Thom Sulanke collaborated to re-investigate squared cylinders. Thom Sulanke rewrote an electrical network program of Stuart Anderson's, and a new plugin for plantri. He was able to generate cyl-nets. Each graph written is 3-connected and is obtained from a (at least) 2-connected planar graph by adding an edge connecting two vertices which are not on the same face. Electrical network node analysis was applied to the cyl-nets to calculate edge currents which give dissected square sizes.
To check if the results made sense Thom Sulanke looked for SPSCs with order 20 or less. In agreement with Augusteijn and Duijvestijn, he found none with order less than 20. He found 18 with order 20. Two of these were the ones they found, 79x79 and 81x81. The other 16 were all 80x80 and can be obtained by combining two cyl-nets and so were not found by Augusteijn and Duijvestijn.
These can be divided into 2 isomer classes. (An isomer in square tiling means a tiling with the same squares arranged differently.)
The first set of isomers 80A consists of eight cylinders, with elements 1, 3, 4, 6, 7, 8, 9, 10, 11, 12, 14, 16, 19, 20, 23, 24, 26, 27, 30, 34.
The second set 80B consists of eight cylinders, with elements 1, 3, 4, 6, 7, 8, 9, 10, 12, 13, 14, 16, 17, 20, 21, 24, 26, 29, 30, 34.
Images of all 18 SPSC of order 20 appear on this page, the 16 new SPSCs appear below, and a PDF of all of them is here.
The investigation by Anderson and Sulanke establishes that there are 18 Simple Perfect Squared-Cylinders (SPSCs) in order 20, that order 20 is the lowest order in which SPSCs can appear, and that the 79x79 SPSC found by Augusteijn and Duijvestijn in 1983 is the smallest size in the lowest possible order .
- REFERENCES.
- R.L. BROOKS, C.A.B. SMITH, A.H. STONE AND W.T. TUTTE. 'The Dissection of Rectangles into Squares'. Duke Math. J. 7 (1940) 312–340.
- A. AUGUSTEIJN AND A. J. W. DUIJVESTIJN,"Simple Perfect Square-Cylinders of Low Order", Journal of Combinatorial Theory, Series B 35 (1983) 333-337
- J. C. WILSON, “A Method for Finding Simple Perfect Squared Squarings,” Thesis, University of Waterloo, (1967).
- A. J. W. DUIJVESTIJN, “Electronic Computation of Squared Rectangles,” Thesis, Technological University Eindhoven, The Netherlands; Philips Research Reports, Vol. 17, pp. 523-612, (1962).
- S. J. CHAPMAN, "The Dissection of Rectangles, Cylinders, Tori, and Möbius bands into Squares", : Duke Math. J. Volume 72, Number 2 (1993), 467-485.
- I. GAMBINI, "Quant aux carrés carrelés", Thesis, "Université de la Méditerranée Aix-Marseille II, (1999).
SPSC 80A (1/8-8/8) Anderson & Sulanke (2012)
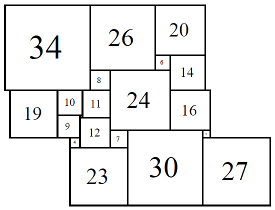
Figure 3; 80x80 (1/8)
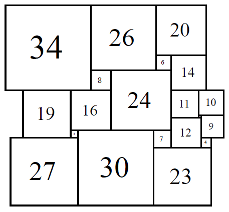
Figure 4; 80x80 (2/8)
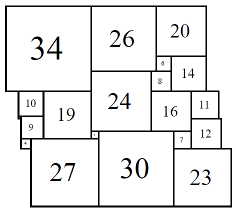
Figure 5; 80x80 (3/8)
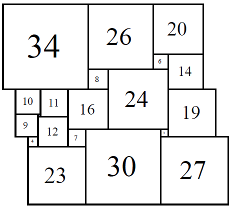
Figure 6; 80x80 (4/8)
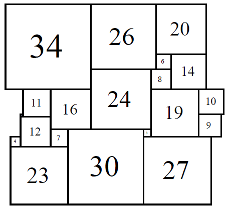
Figure 7; 80x80 (5/8)
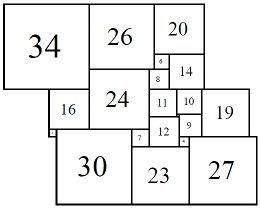
Figure 8; 80x80 (6/8)
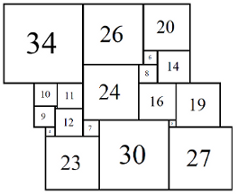
Figure 7; 80x80 (7/8)
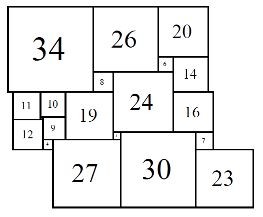
Figure 8; 80x80 (8/8)
SPSC 80B (1/8-8/8) Anderson & Sulanke (2012)
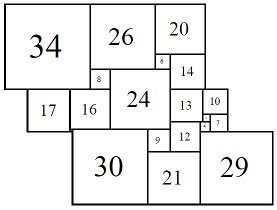
Figure 9; 80x80 (1/8)
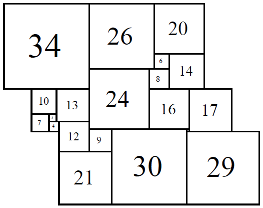
Figure 10; 80x80 (2/8)
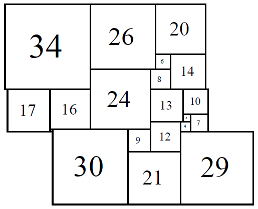
Figure 11; 80x80 (3/8)
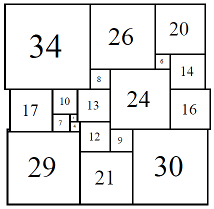
Figure 12; 80x80 (4/8)
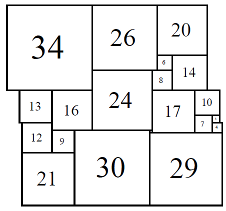
Figure 13; 80x80 (5/8)
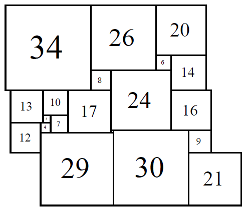
Figure 14; 80x80 (6/8)
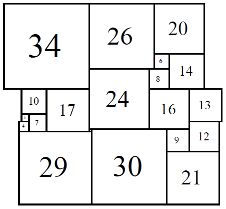
Figure 15; 80x80 (7/8)
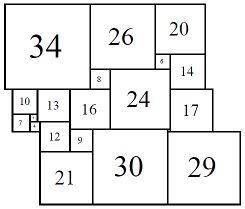
Figure 16; 80x80 (8/8)