Geoffrey H. Morley

G. H. Morley
Geoffrey H. Morley was born in Leicester on 13 November 1944 and attended Wyggeston Grammar School for Boys. He went on to study mathematics and electrical sciences at Christ's College, Cambridge. He worked as a software analyst for the National Coal Board (later known as British Coal), then for Origin until its merger with Atos in 2000.
Until 1964 his only knowledge of squared squares was the one depicted in Kraitchik's 'Mathematical Recreations'. He collected over 1,000 squared rectangles over a 4-year period (1960-64). Some were contributed by other pupils, mostly by Martyn Smith (1946-2007). They knew nothing about the connection with electrical network theory. However, Geoffrey drew some conclusions about the possible numbers of horizontal and vertical line segments, while Roger Burrows observed that, with unreduced elements, when a line segment is replaced by a square its side in the new squaring has the same length as the line segment in the original squaring.
In late 1963, Dr (later Professor) Geoffrey Horrocks, then a mathematics lecturer at Liverpool University and a former Wyggeston pupil, learnt of Geoffrey's interest in squared rectangles from his maths teacher John Hesselgreaves. He knew that Cedric Smith, whom he had once met and also a former Wyggeston pupil, had worked on squared rectangle theory. Geoffrey soon met Geoffrey Horrocks and, separately, Cedric Smith.
Cedric knew that his friend Bill Tutte was planning a visit to the UK in the summer and eventually John Hesselgreaves and Cedric arranged a meeting at the school which was held on 14 June 1964. Three of the Trinity Four (Brooks, Smith and Tutte - Stone was in the US) and two of Geoffrey's maths teachers, John Hesselgreaves (1904-1985) and Roy Mackenzie (1923-1996), were at the meeting. The others present were pupils and former pupils.
Two new methods of constructing simple perfect squares were presented at the meeting. Bill Tutte explained the method that one of his students, John Wilson, had devised and used to construct a simple perfect square of order 25, beating Willcocks's record of order 37. This discovery had already been announced in March.
But first Geoffrey surprised everyone with his method which was published in Eureka [2] in 1967. P.J Federico had this to say in his historical survey article on squared squares and squared rectangles; "A highly ingenious method of constructing simple perfect squared squares of high order, 60 or above, from specially related pairs of squared rectangles, discovered by the author while in high school."[1].
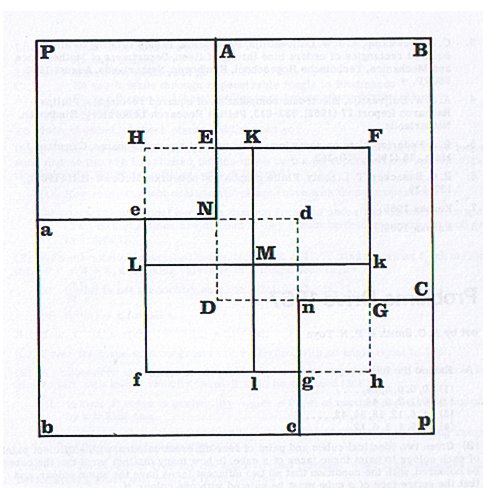
Diagram from 1967 Eureka article illustrating Morley's Method
In the Eureka article, Geoffrey described his method with the aid of the accompanying diagram;
"By means of the so-called rotor-stator method, developed by four members of the Trinity Mathematical Society about 1938, it is possible to construct pairs of mutually congruent but differently squared rectangles, such that they can be oriented to share a common corner element. The addition of two extra squares gives a compound squared square which is generally perfect."
"Few SPSSs were known until I devised a method of constructing an unlimited number of a particular kind. The smallest such solution to date has 60 squares and (reduced) sides 616,457[3]. The method is as follows:
"We start off with the two rectangles HKML, hkMl in the diagram, which possess the properties just described: they are oriented as shown, so that the squares HENe, hGng are congruent. ACBD, abcd are two other rectangles with the above properties; the squares EFGD, efgd are congruent. Clearly, we can scale the two sections of the diagram so that they fit, as shown. Then the square is dissected into the squares of ABCGFE, abcgfe, LMKENe, and lMkGng, together with the squares PANa, pCnc, LMlf, and KMkF. In general this dissection is simple and perfect."
After publication Geoffrey found more solutions. Those SPSSs he found by his method that are displayed on this site are in orders 48, 49, 59, and 60.

Pictured left to right: J.W. Hesselgreaves, R.S. Scowen, R. Mackenzie, M.H. Miller, M.G. Smith, R.F. Burrows, G.H. Morley, ?, R.L. Brooks, ?, W.T. Tutte.
Geoffrey has maintained his interest in mathematics and tilings until the present day. He is in many ways the leading exponent in the area of Isosceles Right Triangled Squares (IRTSs) and has produced an extensive catalogue of IRTSs, rivalling the assembled collection of squared squares in size, order and construction techniques. In addition to their mathematical qualities, one cannot but notice the stunning visual impact and cubist beauty of these dissection tilings. A large part of his collection is on display as part of this site.

Pictured left to right: R.F. Burrows, M.H. Miller, R.S. Scowen, G.H. Morley, ?, M.G. Smith,
?, W.T.Tutte, C.A.B. Smith, R. Mackenzie, R.L. Brooks.
Geoffrey has also made significant recent contributions to the low order catalogue of SPSSs and CPSSs. In 2007 he found close to 300 new SPSSs in order 31. In 2012 he discovered over 500 new CPSSs in orders 29 to 34.
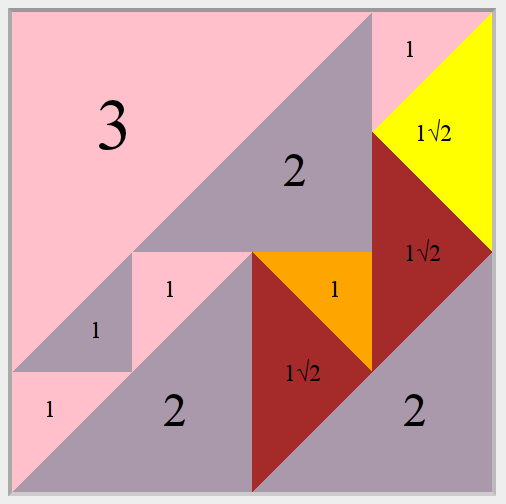
Simple Primitive Imperfect Isosceles Right Triangled Square

Kerrie (cousin), Geoffrey, their maternal
grandmother and Geoffrey's mother
- Squaring Rectangles and Squares, A Historical Review with Annoted Bibliography, P.J. Federico, footnote 57
- Networks and Squared Squares, G.H. Morley, Eureka (J. Archimedeans, Cambridge Univ. Math. Soc.) No. 30, Oct. (1967) 14-16.
- Correction - side of 616457, wrongly stated in the article in [2] to have side 616,467.
- OEIS: A174386 Smallest possible area for a perfect isosceles right triangled square of order n; or 0 if no such square exists.