Square Packing & Squaring the (Double) Plane

Adam Ponting's work in Square Tilings

Adam - "I wrote a program to find if there were packings for squares of side \(1,2,3 \dots n^2\) . Packings? I don’t know what to call them – unlike the business of squaring squares and rectangles, I’m not concerned about the shape of the boundary. The program found packings for \(9, 25 \) and \(49\) squares, and there’s a simple regular pattern that can be extended to work with any odd \(n^2\)."

Often, in mathematics, when it is not possible to make progress on a field of research, or in solving a particular problem, a good strategy to proceed is to relax one of the constraints that defines the problem. In the case of squared squares and square tilings generally, one of the main problems has been the search for 'perfect' square tilings, that is every square in the tiling should be a different size. The most 'perfect' tiling would be one that uses all integers from \(1\) to \(n\). We know that the only consecutive sum of squares from \(1\) that adds to a square number is the sum of the integers \(1^2+2^2+3^2+ \dots +24^2 = 70^2\). However it has been proved that such a tiling is not possible, except in the 24 dimensional spaces of the Leech lattice. This seemed to put a end to the possibility of constructing such a perfect tiling in 2D.

However, what if like Adam, we relax the condition that we have to tile, or dissect into squares, a particular geometric shape such as a square, rectangle, cylinder or torus? What if we are not concerned about the shape of the boundary?

The square tilings constructed by Adam Ponting create simple 'perfect' square tilings from size \(1,2,3 \dots n^2\), where \(n\) is an odd number. By choosing larger and larger \(n\), the result is a tiled area greater in size than any specified area, – which is close to what infinite means. It’s done by using an \(n^2\) arrangement of squares, with any odd \(n\), e.g. with \(n = 3, 5, 7, 9, 11 \dots \) corresponding to squares up to \(9, 25, 49, 81, 121 \dots \) and each \(n^2\) arrangement of squares is constructed similarly as follows;

How to number the squares:

Begin at bottom right corner of an \(n × n \) square grid. Number every second square leftwards across the bottom row, in a checkerboard pattern, i.e. 1, (gap), 2, (gap) \(...\) Then across second bottom row. Continue R to L across every row. Finish at top left with \( (n^2+1)/2.\)
Start at top right, going down the columns, filling the remaining gaps, and moving R to L. i.e. first the rightmost column. Top square is already filled, put \((n^2+3)/2\) in the second row, the next number in the fourth etc.

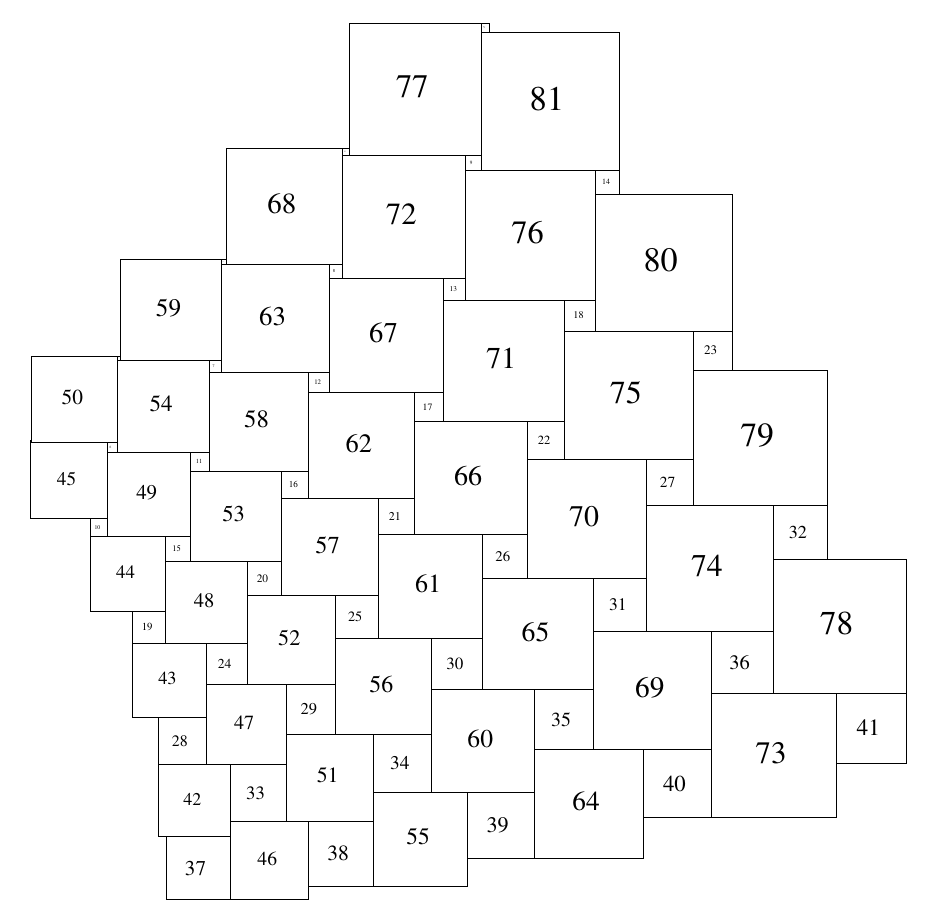
To illustrate the method, see it applied for \(n = 5\) to a \(5×5\) matrix of the integers from \(1\) to \(25\):

Squares are arranged with what Adam calls alternating h-lines and v-lines, shown as black lines in the picture. An h-line is a horizontal line segment with two squares on each side of it, a v-line, a vertical line segment with two squares on each side. The arrangement has a h-line on the top left, v-line on the top right.

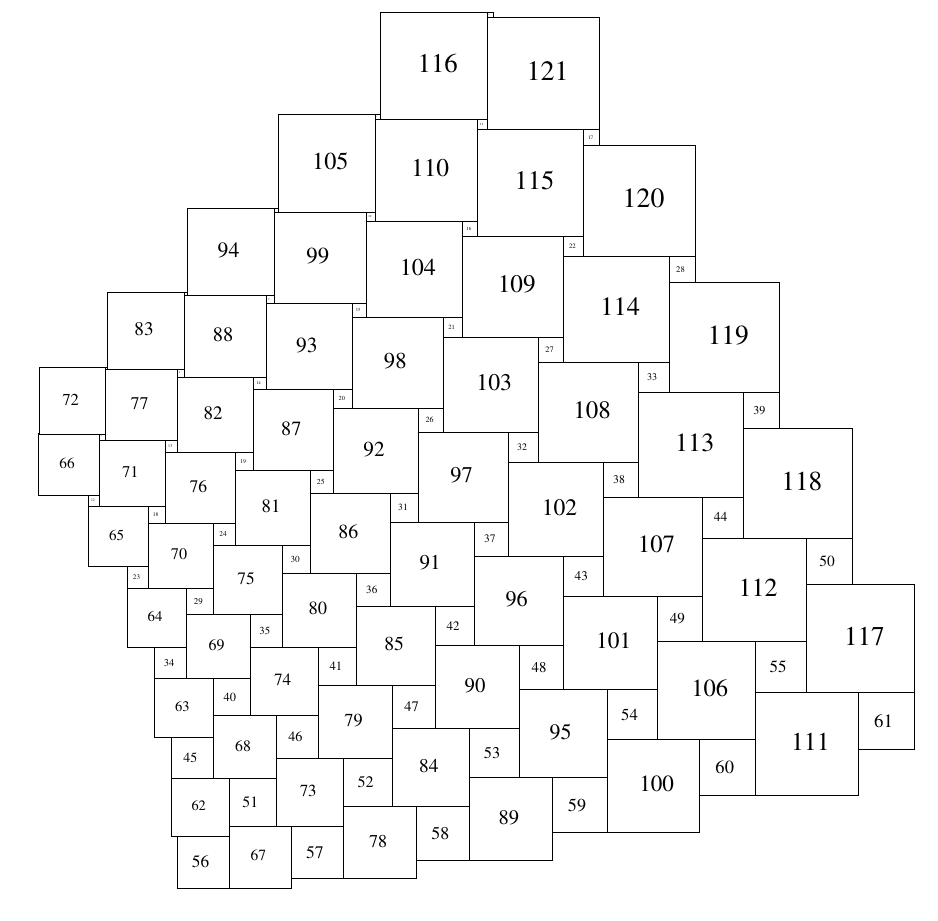
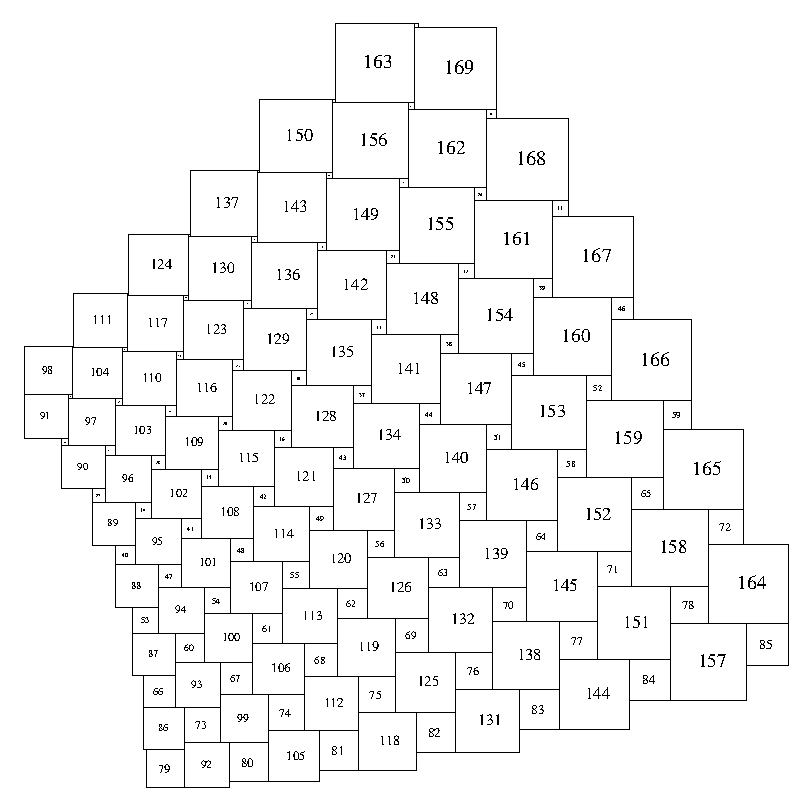
Some more examples for \(n = 9,11,13 \) (though these are oriented differently to the \(5\) above)

Squaring the Plane

Though Adam's construction can be used with any odd n^2, covering an arbitrarily large area, any particular square packing is still of finite size

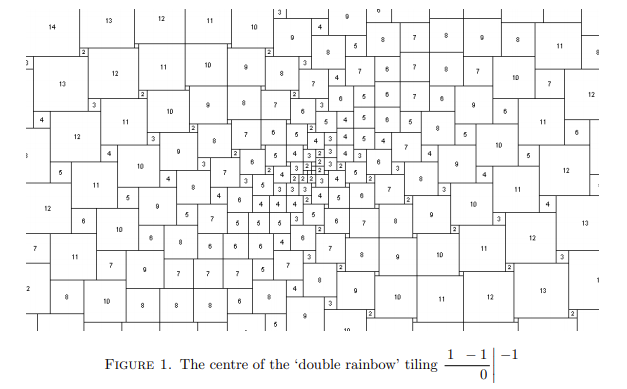
Adam tried to extend some of his square packings into a plane tiling by continuing their arithmetic sequences, but they didn't fit together, along a single radial seam. By generalizing the grid method of construction, he found related grids that do tile the plane - the first being the ‘double rainbow’ tiling (Figure 1) - and recently he has been studying and exploring many variations to this type of tiling, made from grids filled with arithmetic sequences of integers. It turns out that every non-trivial tiling made with sequence grids doubly tiles the plane, and the apparent "not fitting" of extended square packings was the squares of the 2 layers not being aligned. He found the rules that govern when these layers are aligned and when not.

It should be noted that although these extended square tilings tile the plane, they are no longer 'perfect' as multiple copies of the same sized squares exist in the tiling.

Adam wroteup his findings on squaring the plane in a paper on sequence grids & tilings : square tilings paper.pdf [7]

How to construct double rainbow tesselations

They’re built with alternating h-lines and v-lines. An h-line consists of four squares, two on either side of a horizontal line, with equal sums \(a+b=c+d\) and aligned edges. The tesselation is first written in digits on a square grid marked with lines like a wire screen door, then constructed by drawing any h- or v-line from the grid and working outwards from there.

Start with any h-line: e.g. \(3+4=2+5 \):

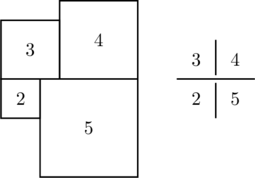
Extend the arithmetic progressions along the diagonals:

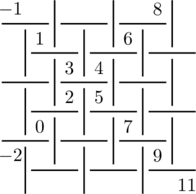
Then fill in a diagonal next to one of these 2, with any arithmetic progression. e.g:

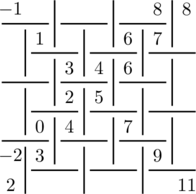
All the empty squares have now been determined and can be filled in, making the sums \(a+b=c+d\) equal across all line segments (the h-lines and v-lines). Then when drawing the tesselation, draw the squares of negative size on the other side of the line from where they ‘should’ be, e.g. \(2+5=10-3 \):

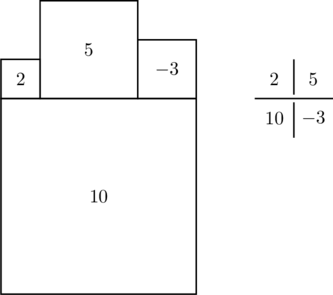
It seems that any grid of numbers constructed this way makes a tesselation of the plane. Also, it seems that all the 0-sized squares (marked them with a small circle) lie in a straight line in the tesselation, no matter what sequences are used. The square packings found a few years ago are each a subset area of one of these tesselations, where there’s only 1 of each sized square.

Square Packing & Squaring the (Double) Plane

Adam Ponting's work in Square Tilings

Squaring the Plane

How to construct double rainbow tesselations

References