Squaring the Plane I

The question was first posed by Solomon Golomb in a 1975 article in the Journal of Recreational Mathematics [1]. He asked if the infinite plane can be tiled by different squares with every positive integer side-length represented. He called it the “heterogeneous tiling conjecture” and asked readers if they could find a solution.

Martin Gardner wrote a number of times about the problems concerned with tiling squares in his 'Mathematical Games' / Mathematical Recreations' column in Scientific American.

Martin Gardner also published collections of his columns, and the solutions sent in by readers in a series of books beginning in 1961[2]. In 'Fractal Music, Hypercards and More ...' (1992) [3] Gardner mentioned

"I gave a way to tile the plane with distinct integer-sided squares based on the dissection of a square into 21 unequal squares (using Duijvestijn's 1978 discovery of 21:112A). Another way to do it is to start with a unit square so dissected, then whirl around it squares of 1,2,3,5,8,13,... in the Fibonacci sequence. However, Gardner noted "Golomb's problem of tiling the plane with consecutive squares, starting with 1, remains unsolved. However, Brian Astle, of Princeton, New Jersey, wrote to explain how the plane could be tiled with consecutive squares in such a way as to leave an arbitrary small fraction of the plane untiled. Every tile in the sequence is at a finite distance from the origin point. Astle's method, too complicated to explain here, remains unpublished. Golomb tells me that he may have found an algorithm for solving his problem, but there are still gaps in the proof that he has yet to fill."

Grunbaum and Shepard wrote about the problem in their 1987 book ¨ Tilings and Patterns [4]. They described there a second way in which a squared square S can generate a tiling of the plane (in addition to the method indicated in the present paper): Take a second copy of S and expand it to a square S1 such that the smallest square in S1 is the size of the original square S and fit S into that square. Take another copy of S and expand it to S2 so that its smallest square is the size of S1, and so on.

In 2008 Fred Henle and James Henle published a solution [5]. Their approach focuses on rectangles and ells. By “ell,” they mean any six-sided figure whose sides are parallel to the coordinate axes.

A figure is perfect if it is composed entirely of squares of different sides. The key to their result is a Lemma, which states that given any perfect ell, it is possible to add squares to it to form a perfect rectangle. When they add squares to a perfect figure, keeping it perfect, they say they are “puffing it up.” When they puff an ell up to form a perfect rectangle, they say they are “squaring up the ell.” They can then “square the plane” as follows:

1. Start with any perfect ell and square it up.
2. Create a new ell by attaching to the rectangle the smallest square not yet used.
3. Square this ell up, making sure that new squares are added in all four directions.
4. Repeat steps 2 and 3 ad infinitum.

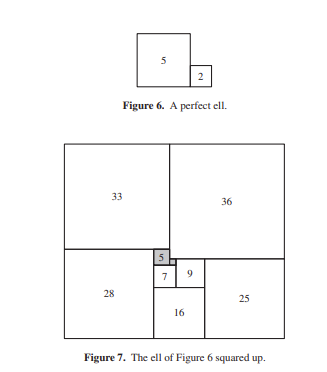
Henle and Henle noted ;

The algorithm presented in this paper is extravagant in that the ratio of the largest square used so far to the smallest square not yet used rapidly diverges. The procedure for squaring up, for example, when applied to the smallest possible ell, a 2 × 2 square next to a 1 × 1 square, ends in a rectangle with dimensions 1106481365205154721693 × 2659648557852203795117. The smallest square not used at this point is 4 × 4. The squaring-up procedure can certainly be improved. By way of illustration, take the ell in Figure 6. .... Our procedure, however, doesn’t square the ell up until a rectangle is reached with dimensions approximately (5.0 × 1014272) × (5.8 × 1014272). Can our squaring-up procedure be improved in some well-defined way? Does an algorithm exist for tiling the plane that methodically expands a connected island of squares in such a way that the ratio of the largest square used to the smallest not yet used is bounded by a polynomial?

Henle and Henle also posed a number of other questions and problems related to squaring of the plane, some of which they subsequently solved;

• Simple tilings. A perfect figure is simple if it contains no perfect subrectangle. Our tiling is far from simple. Is there a simple tiling of the plane using one specimen of each integral side? - In section 4 of [7] Henle and Henle construct a simple, perfect, square-tiling of the plane.
• The half-plane and quarter plane. Can the half-plane be squared? Can the quarter- plane be squared? We are especially interested in this question because if it is possible to tile a quarter plane four times using, altogether, every integral square just once, then it’s possible to tile the plane using all the integral squares plus one square of any given side (say π).
  - No solution to tiling the half and quarter plane has been found using all the integral squares.
• Rational squares. The algorithm of our theorem can easily be used to tile the plane using one square of every rational side. As with integral squares, we don’t know if similar procedure works for the half- or quarter-plane.
• Positive and negative squares. We can tile the plane with squares whose sides are natural numbers and with squares whose sides are rationals. What about squares whose sides are (positive and negative) integers? We interpret the effect of placing a small negative square on top of a large positive one as removing a part of the large square. Once again, our algorithm works easily for this. Just as placing a positive square next to a rectangle creates an ell, so does placing a negative square on a corner of a rectangle. With care, no point of the plane will be touching more than three squares (one negative, two positive).
  - A tiling of the half-plane with positive and negative side lengths has been constructed [7]
• Odd squares. Can the plane be squared with all the odd squares? This seems unlikely to us. Can the plane be squared with some of the odd squares? In general, what well- defined subsets of the natural numbers can be used to tile the plane?
  - It has been found that the set of odd numbers do not tile the plane [7]
  - It is now known that a set with one or three odd numbers may tile the plane but a set with two odd numbers can't.[6][7]
  - It is also shown that a set growing faster than the Fibonacci numbers cant tile the plane.[6][7]
• Coloring. Neither our tiling nor the Fibonacci tiling can be 3-colored. Is there a 3- colorable tiling of the plane using exactly one square of each integral side?
  Is there a simple algorithm for 4-coloring the tiling described in this paper?
Can space be cubed?.
• Triangles. Scherer proved[8] that the plane cannot be tiled with equilateral triangles of different sizes if one triangle is smallest. He has found a way of tiling the plane, however, with different sizes of iscoceles right triangles and with enlargements of certain other triangles. Pomerance proved that it is possible to tile the plane with one rational triangle of each congruence class such that any two neighboring triangles share either an entire side or just a vertex . Left open is the question: Can the plane be tiled with all rational equilateral triangles so that no triangle has an infinite number of neighbors?

References

1. S. W. Golomb, The Heterogeneous Tiling Conjecture, The J. of Rec. Math. 8 1975.
2. M. Gardner, The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection, Simon and Schuster, New York, 1961
3. M. Gardner, Fractal Music, Hypercards and More ... , W. H. Freeman, New York, 1992
4. B. Grunbaum and G. C. Shephard, ¨ Tilings and Patterns, W. H. Freeman, New York, 1987
5. Frederick V. Henle and James M. Henle, “Squaring the Plane,” The Am. Math. Monthly, 115(1): 3-12, 2008.
6. A. Berkoff, J. Henle, A. McDonough, A. Wesolowski, "Possibilities and Impossibilities in Square-Tiling", Int. J. of Comput. Geom. & Apps., Vol. 21, No. 5 (2011)
7. F.V. Henle and James Henle, "Squaring and Not Squaring One or More Planes", Online Journal of Analytic Combinatorics, 01: 1-18, 2015
8. Karl Scherer, New Mosiacs, privately printed, 1997
9. James Henle's website