SPSSs Order 33 :

Simple Perfect Squared Squares of Order 33.

There are 378197 simple Perfect Squared squares of order 33. The complete enumeration of this order was produced by Jim Williams in June 2014.

SPSSs of Order 33 are provided as a zipped postscript file (20 SPSSs to a page) spsso33.ps.zip

also the Bouwkampcodes of the SPSSs of order 33.

and the tablecodes of the SPSSs of order 33..

The exploration and enumeration of the SPSSs of order 33.

Ian Gambini

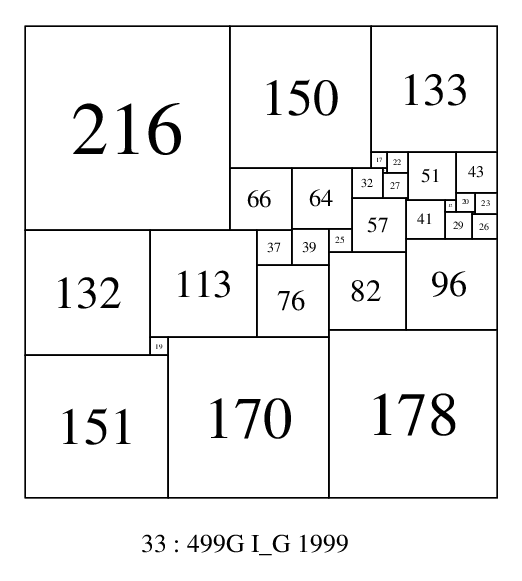
Prior to 2010, this order of squared squares was almost totally unexplored. Ian Gambini had contributed one order 33 SPSS in his 1999 thesis (see figure 33:499G).

Stephen Johnson

Stephen Johnson had explored SPSSs and CPSSs in the orders 30 to 36, with a new semi-random search method using both geometrical and network graph methods. By 2011 he had found 491 SPSS, and 62 CPSS. Further discoveries were made in 2013. In order 33 Stephen Johnson found 36 SPSSs.

A selection of Stephen Johnson's SPSSs of order 33

Jim Williams 2013, 2014, Milla & Anderson 2013

In January 2013 Jim Williams created squared squares of orders 30s and 40s by combining smaller electrical graphs at exactly 3 nodes and filtering out non-solutions. He found an incomplete 142,879 SPSSs in order 33.

Later in the same year, Milla and Anderson completed orders 31 and 32 and found a number of discoveries in higher orders, including 13,715 new discoveries in order 33 SPSSs.

In 2014, with revised and rewritten software running for 2 weeks, Jim Williams enumerated all of order 33 SPSSs, finding a complete total of 378,197 including 221,566 new discoveries.

Some Facts and Figures on the SPSSs of Order 33

The number of SPSSs in order 33

There are 378197 SPSSs in order 33.

378197 = 131×2887 (2 distinct prime factors)

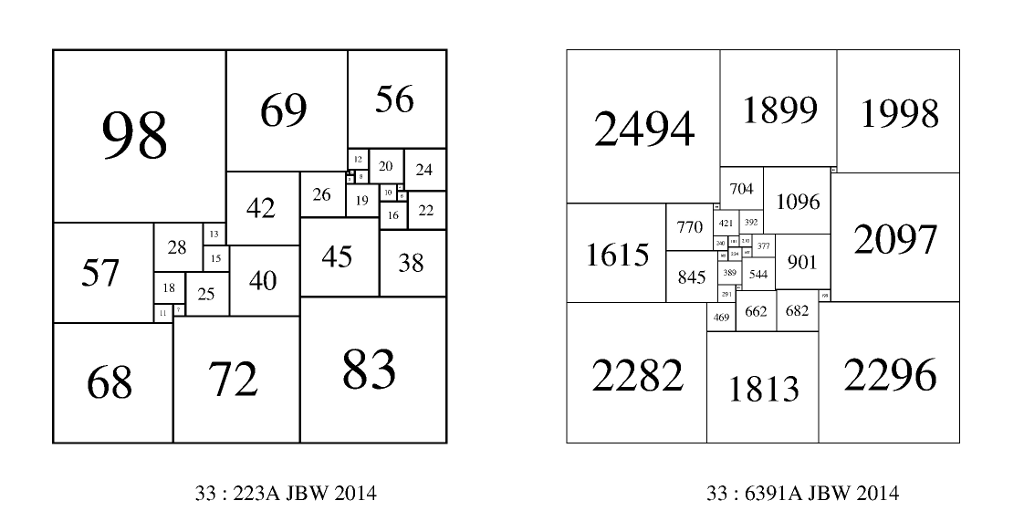
Smallest and Largest SPSSs of order 33

The smallest and largest SPSSs of order 33 are, respectively;

Sub-200s (Subbicentennials)

No sub-200s, (or subbicentennials) - SPSSs with a side less than 200 - exist in order 33. Perhaps all sub-200 SPSSs have been found, but there is no proof that this is the case. The sum of squares formula gives an upper bound on the order size of 48 for a sub-200 perfect square dissection. This bound is larger what the experimental evidence suggests the true bound will be. There are 2 sub-200s in order 32 (185 & 199) and then there are none in orders 31-28. The remainder exist in SPSS orders 21-25 and 27. The catalog of CPSSs is complete to order 36, thanks to Jim Williams, and the only known sub-200 CPSS is 24:175. There are 27 known sub-200s (including 24:175 once).

The distribution of SPSS sizes in order 33

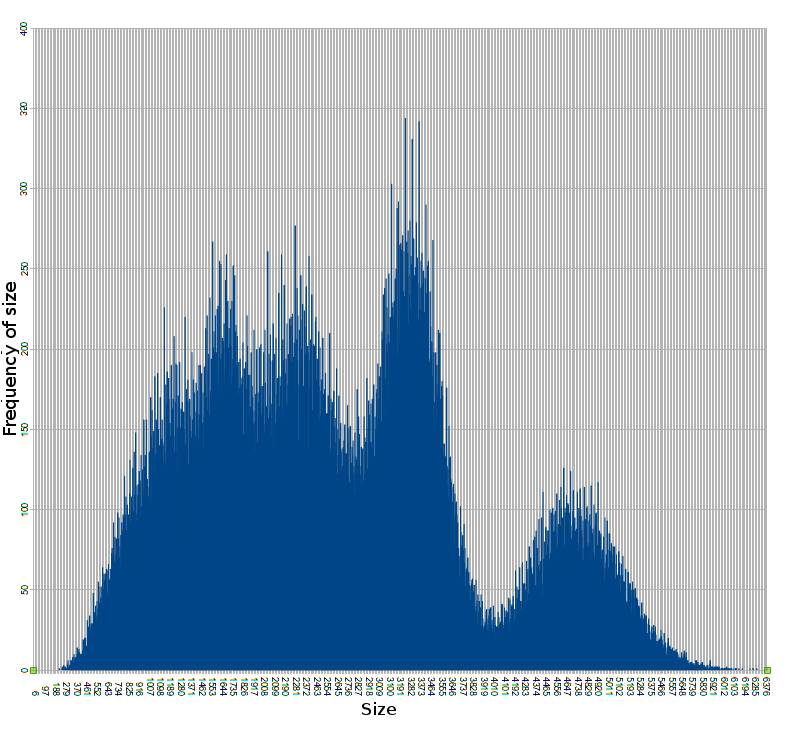
The peaks and troughs invite explanation and closer inspection of the data.

Measures of central location of size in the SPSSs of order 33.

The mean (or average) size is 2667.

The mode, the most frequently occuring size, is 3240, the highest peak of the graph, with 344 SPSS. From the graph of SPSS size and frequency we can see peaks at around 1520 and 2280. There are also troughs at around 2700 and 4000, and a smaller peak of larger sizes in the 4 and 5 thousands.

The median, the middle size in a lineup from smallest to largest, is 2546.

This kind of distribution shape of sizes is common to all SPSS orders, it appears more detailed, and the sizes scale up as the order increases.

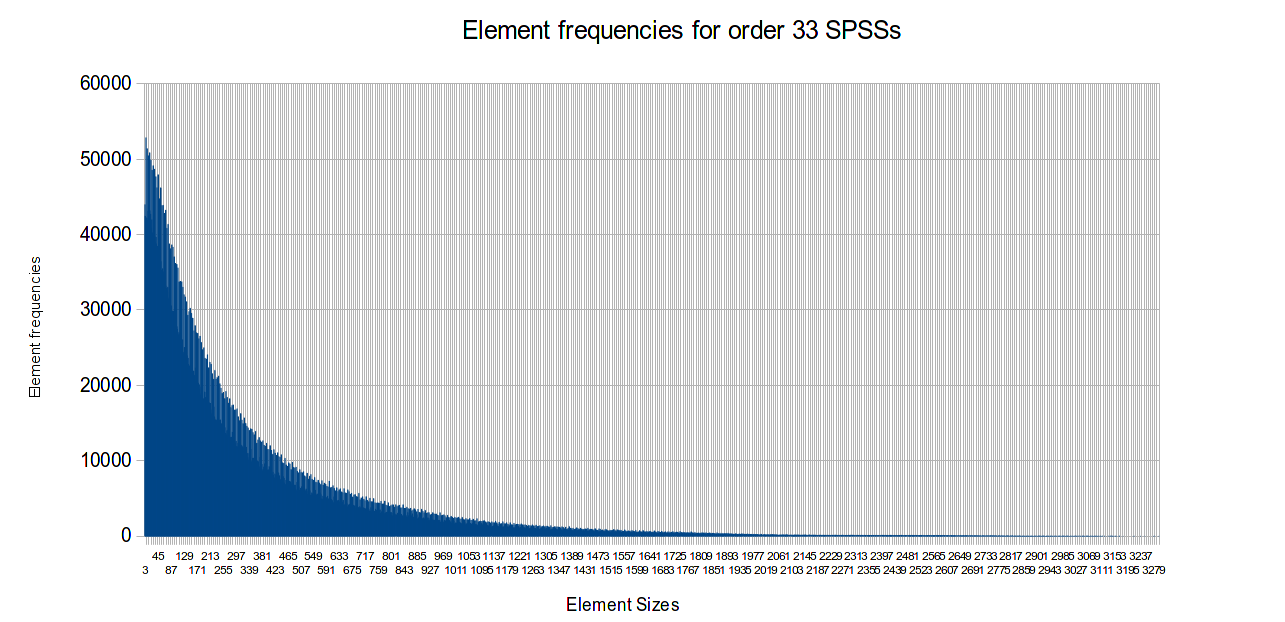
The distribution of element sizes in order 33 SPSSs

A count of element sizes gives a decay curve. Closer inspection reveals higher frequencies for element sizes which are multiples of 4.

Crosses in order 33 SPSSs

The appearance of a cross in a SPSS is a rare occurance. There are 838 SPSSs with crosses in order 33, about 0.22% of the total of 378,197.

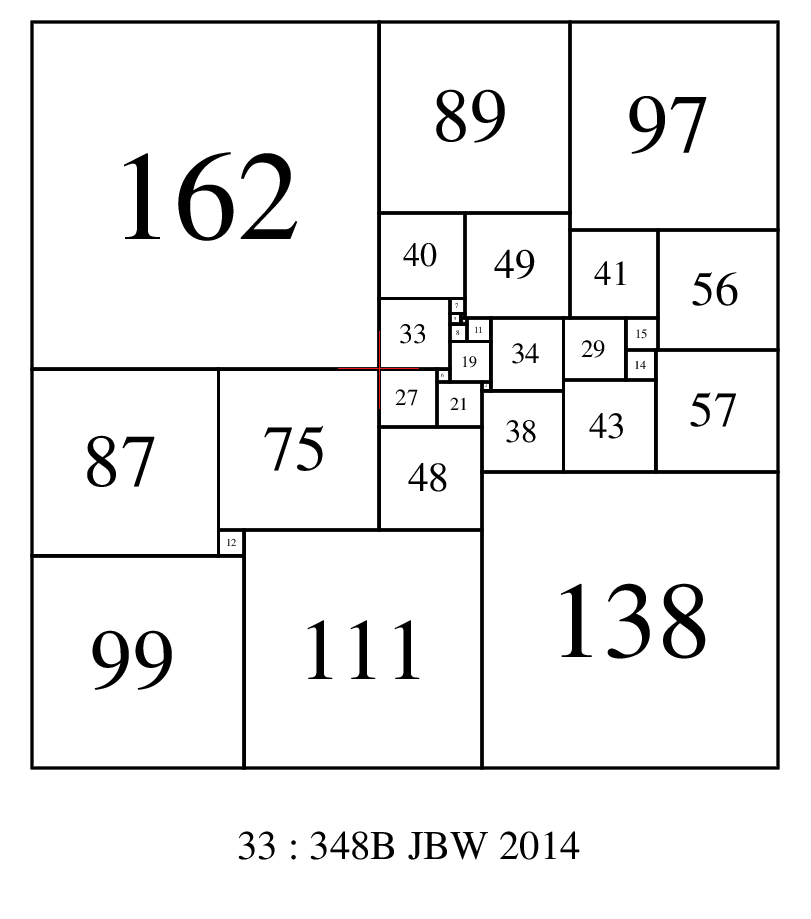
Largest element not in a corner in order 33 SPSSs

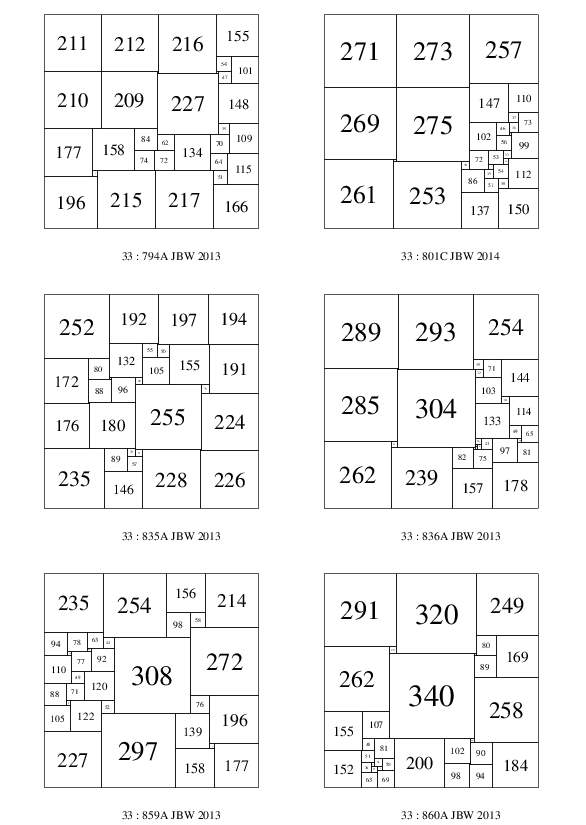
In most SPSSs, the largest element is situated in a corner, indeed the appearance of the largest element not in a corner is a rare occurance. There are 317 SPSSs with the largest element not in a corner in order 33, about 0.0838% of the total of 378,197. Here's a selection of the order 33 SPSSs with the largest element not in a corner. The first SPSS 33:794A has all 5 of the largest elements not in a corner.

Nicest SPSS in order 33

Most SPSSs have elements which vary greatly in size from the smallest to the largest element. If this variation in element sizes can be restricted then all elements can be clearly seen and we can call such SPSSs 'nice'. A measure of 'niceness' is the ratio of size of the largest element to the size of the smallest element. In May 2014, Jim Williams found an order 33 SPSS with a largest/smallest element ratio of 549/70 = 7.8429, making this the 'nicest' known perfect squared square.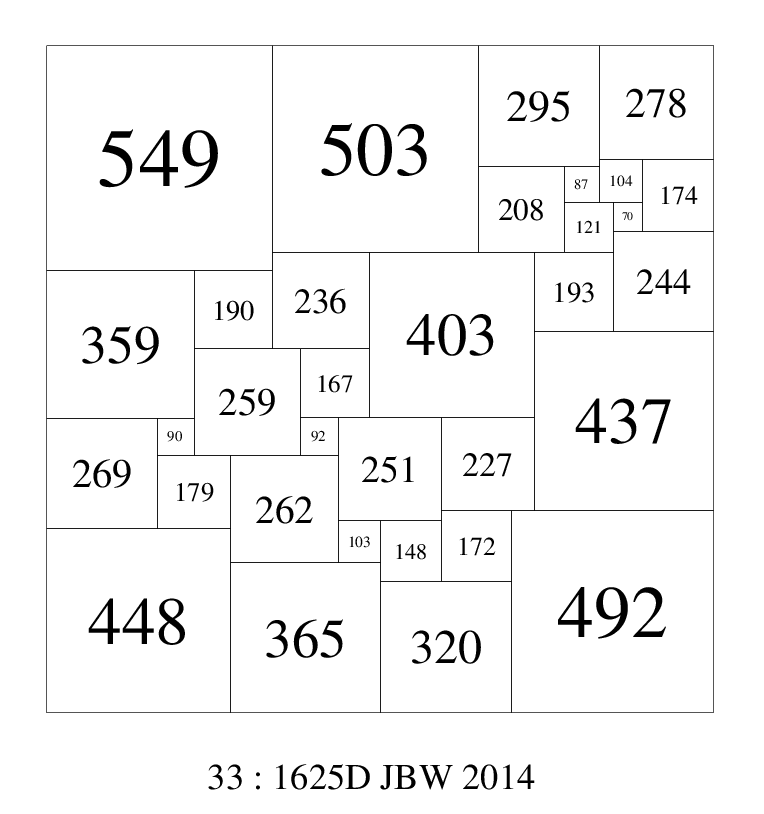

'nicest' known SPSS with the same ratio of largest element to smallest element of 549/70 = 7.84