(1) SPSS, Order 21; spsso21.pdf

The search for the Perfect Square with the smallest number of distinct squares (the lowest order) had been ongoing since the late 1930's.

• In 1940 R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T.Tutte published 'The Dissection of Rectangles into Squares"[11] , referring to an order 55 simple perfect squared square (SPSS), side 5468 using theoretical methods involving the use of symmetry in electrical networks. Their new techniques and theoretical work led R.L. Brooks to the discovery simple perfect squared square (SPSS), side 4920 of order 38, which was an improvement on the first Perfect Squared Square of order 55, side 4205 (a compound perfect squared square - a CPSS) found by R. Sprague in 1939.
• In 1962 C.J. Bouwkamp and A.J.W. Duijvestijn finished their computer squared square search. They applied Tutte's Wheel Theorem and generated c-nets, used an isomorphism reduction technique to reduce duplicate graphs, then produced complete catalogues of squared rectangles by order from the c-nets using electrical network theory. The squared rectangles catalogues were examined for perfect squared squares. Duijvestijn published his PhD thesis 'Electronic Computation Of Squared Rectangles'[8] in 1962 and showed that no SPSS exists with fewer than 20 squares.
• In 1963 P.J. Federico published 2 CPSSs of order 25 (with sides 235 and 344) that he constructed using transform techniques.[3]
• In 1964, J.C. Wilson a student of Tutte's, found an SPSS with side 503 of order 25 using a new method.[12]
• In 1967 J.C. Wilson developed his method into a computer algorithm which he published as his thesis[4]. Included in his PhD thesis were 5 new SPSSs of order 25 (including the one he found in 1964) and 24 new SPSSs of order 26.
• In 1973 N.D. Kazarinoff and R. Weitzenkamp published a paper which proved that a compound perfect squared square (CPSS) must contain at least 22 subsquares.[13]
• On March 22 1978, A.J.W. Duijvestijn, found a single SPSS with 21 squares in his computer search of 22 edge c-nets [1][5][6]. Duijvestijn's order 21 : 112A is order minimal and unique. An image of the tiling is below, a pdf link above and a javascript display menu can be found by clicking the link to the left.
• In August 1979 Paul Leeuw completed his thesis 'Compound Squared Squares'[14][15]. Using ideas of Federico and computer programs of Duijvestijn and newly written software Leeuw proved that the smallest CPSS is Willcocks order 24 175 side CPSS, thereby confirming Duijvestijn's order 21 side 112 SPSS as the lowest order perfect squared square. The thesis was rewritten and published as a joint paper by Federico, Duijvestijn and Leeuw in 1982[16].

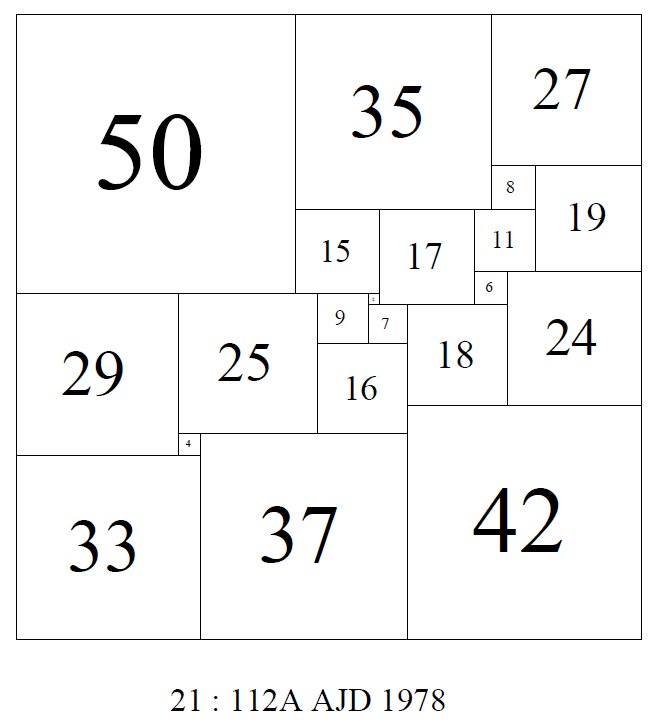
From Duijvestijn's 1978 paper [5] reporting the discovery;

"This note is to report the existence of a simple perfect dissection of a square into 21 unequal squares.";

"The dissection was found in the night of March 22, 1978 with the aid of the DEC-10 computer of the Technological University Twente, The Netherlands. Since no simple perfect squared squares were found of orders less than 21, it is a simple perfect squared square of lowest order . Also, it is the only simple perfect squared square of order 21. So far, the lowest order simple perfect squares known, are of order 25, the first one of which, due to Wilson, was published in [4]. In total 5 simple perfect squarings of order 25 were published in Wilson’s thesis [4]. Later another 3 simple perfect squarings of order 25 were obtained by Federico [2]. The lowest order compound perfect square is still the single 24 order perfect square found by Willcocks [10] in 1948. In my thesis [8] the investigation of all 3-connected graphs of orders up to and including 20 was reported. No perfect squarings were found at that time. The Bouwkampcode [9] of the present squaring reads as follows; (50, 35, 27) (8, 19) (15, 17, 11) (6, 24) (29, 25, 9,2) (7, 18) (16) (42) (4, 37) (33). The dissection was obtained from a 3-connected planar graph of order 22 with complexity 75264. The reduction factor is 336. The reduced side of the square is 112.[5]"

1. A. J. W. DUIJVESTIJN, A Lowest Order Simple Perfect 2 x 1 Squared Rectangle, J. Combinatorial Theory B 26, (1979), 372-374
2. P. J. FEDERICO, private communication; Squaring rectangles and squares. A historical review with annotated bibliography, Submitted to the congress on graph theory held in July 1978 on the occasion of the 60th anniversary of Professor Tutte.
3. P.J. FEDERICO. Note on some low-order perfect squared squares. Canad. J. Math. , 15:350–362, 1963.
4. J. C. WILSON, “A Method for Finding Simple Perfect Squared Squarings,” Thesis, University of Waterloo, 1967.
5. A. J. W. DUIJVESTIJN, Simple perfect squared square of lowest order, J. Combinatorial Theory B 25 (1978), 240-243.
6. A. J. W. DUIJVESTIJN, Fast calculation of inverse matrices occurring in squared rectangle calculation, Philips Res. Rep. 30 (1975), 329-336.
7. A. J. W. DUIJVESTIJN, Two simple perfect squares of order 22, Memorandum No. 230, Twente University of Technology, September, 1978.
8. A. J. W. DUIJVESTIJN, “Electronic Computation of Squared Rectangles,” Thesis, Technological University, Eindhoven, The Netherlands, 1962; Philips Research Reports 17 (1962), 523-612.
9. C. J. BOUWKAMP, On the dissection of rectangles into squares, Proc. Kon. Ned. Akad. Wetensch. Amsterdam 49 (1946), 1176-1188; 50 (1947), 58-71, 72-78.
10. T. H. WILLCOCKS, Problem 7795 and solution, Fairy Chess Rev. 7 (1948), 106.
11. R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T.Tutte 'The Dissection of Rectangles into Squares', Duke Math. J. 7 (1940) 312–340
12. W. T. TUTTE, Squared rectangles, pp. 3-9 in “Proceedings of the IBM Scientific Symposium on Combinatorial Problems, held on March 16-18, 1964, at the Thomas J. Watson Research Center, Yorktown Hights, N.Y.”
13. N.D. KAZARINOFF and R. WEITZENKAMP. On the existence of compound squared squares of small order. Journal of Combinatorial Theory B , 14:163–179, 1973
14. P. LEEUW. Compound Squared Squares. Bachelor’s thesis, Technological University Twente, August 1979.
15. P. LEEUW. Compound squared squares : programs. Technische Hogeschool Twente, Onderafdeling der Toegepaste Wiskunde, 1980.
16. A.J.W. DUIJVESTIJN, P.J. FEDERICO, and P. LEEUW. Compound perfect squares. The American Mathematical Monthly, 89(1):15–32, January 1982.