Faultfree Perfect Squared Projective Planes (FPSPPs)
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin.
A projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two lines in a projective plane intersect in one and only one point.
Renaissance artists, in developing the techniques of drawing in perspective, laid the groundwork for this mathematical topic.

Parallel lines intersect
in the vanishing point at infinity.
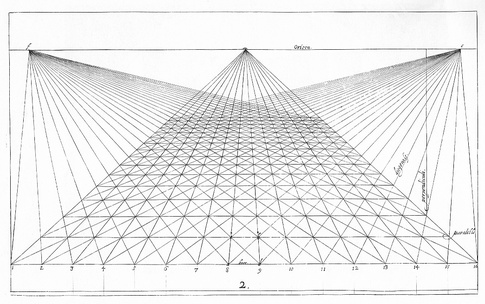
Perspective with vanishing points at the line at infinity.
The plane is also often described topologically, in terms of a construction based on the Möbius strip: if one could glue the (single) edge of the Möbius strip to itself in the correct direction, one would obtain the projective plane. (This cannot be done in three-dimensional space.) Equivalently, gluing a disk along the boundary of the Möbius strip gives the projective plane. Topologically, it has Euler characteristic 1, hence a demigenus (non-orientable genus, Euler genus) of 1.
Since the Möbius strip, in turn, can be constructed from a square by gluing two of its sides together, the real projective plane can thus be represented as a unit square (that is, [0,1] × [0,1] ) with its sides identified by the following equivalence relations:.
(0, y) ~ (1, 1 − y) for 0 ≤ y ≤ 1.
and.
(x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1,.
as in the diagram below.
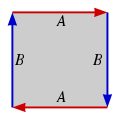
The fundamental polygon
of the projective plane.
We are interested in dissecting the surface of the fundamental polygon when it is a square, (or rectangle with the same gluing instructions), into a finite number of smaller squares, called the elements. As the real projective plane has no boundary, the edges of the square elements of the dissection can be parallel with edges of the fundamental polygon, but need not coincide with them, or the edges of the square elements can be at 45 degrees to the rectangle sides. If the edges of elements and fundamental polygon are parallel then the elements are commensurate with the rectangle edge sizes, alternatively, if they are at 45 degrees then the rectangle edges are multiples of √2.
In both cases the sizes of the elements are commensurate with each other and can be expressed as integers divided by any common factor. If the sizes of the elements dissecting a projective plane are all distinct, (no two the same size), then we call the dissection perfect. The number of elements in the dissection is called the order. We call a tiling faultfree if has no fault line, which is what we call a glued edge that does not intersect any tiles. We use the abbreviation FPSPP for Faultfree Perfect Squared Projective Plane.
All of these projective plane dissections have been discovered recently by Geoffrey Morley and assembled by him into this collection. Geoffrey has also authored some postscript programming code which is the basis for the dissection graphics on this page. Stuart Anderson has also contributed to the programming code. This is currently an active area of research, all known updates are included here as of 26th March 2014.
The dissections are available as as 2 files in both ps FPSPPs2-5.ps and FPSPPs6-7.ps , and pdf FPSPPs2-5.pdf and FPSPPs6-7.pdf and in SVG/HTML pages, linked from the menus on this page.
Known FPSPPs (all in the attached files excluding any of order>5 with sloping tile sides):
| Order | Nonsloping tile sides | Sloping tile sides |
|---|---|---|
| 2 | 1 | 0 |
| 3 | 3 | 2 |
| 4 | 4 | 10 |
| 5 | 8 | 93 |
| 6 | 24 | ? |
| 7 | 65 | ? |
The FPSPPs of orders 6 and 7 on the website do not include any with sloping tile sides, of which there must be hundreds.
There may be over 500 of order 6 and thousands of order 7.
The elements (5,7,9,13,21) of FPSPP 5: 25.5R2 x 15R2 A are all odd (this is impossible for simple perfect squared rectangles (SPSRs), why?, see here) . It is not known whether there are any other FPSPPs with no even element.
Order 5 has an example of a 2 x 1 FPSPP (5: 10√2 x 5√2 A).
Orders 3, 4 and 5 have instances of two FPSPPs, one with sloping tile sides and the other without, whose elements are the same. The situation is unknown for higher orders.