SPSSs Order 37;
The first SPSS of this order was found by Willcocks, with a side of 1947 (see illustration). Willcocks claimed the year of discovery as 1947 [1], but this was questioned by Bouwkamp [2], Willcocks was asked it about didn't recall anything about this square (in 2012). [3]. Martin Gardner gave the year of discovery of 37:1947 as 1959 [4]. The order 37:1947 was based on Brook's order 38:3920, "by a slight modification of the method used" [1]. The first publication of the Brooks 38:2920 discovery was in 1950 by W.T. Tutte [5]. The next 2 SPSSs of this order were found by Ian Gambini in the late 1990s [6]. In 2013 Milla and Anderson found 282 and in the same year James Williams found 99746. In 2014 Brian Trial found 171.
In July 2020 Jim Williams announced that he had completed enumeration of order 37 SPSSs. There are 17086918 SPSSs in this order.
The following listings have the names of the person (or persons) who discovered each SPSS.
Listings; Bouwkampcodes spsso37.bkp.zip and tablecodes spsso37.txt.zip and postscript spsso37.ps.zip Each listing is over a Gigabyte in size compressed.
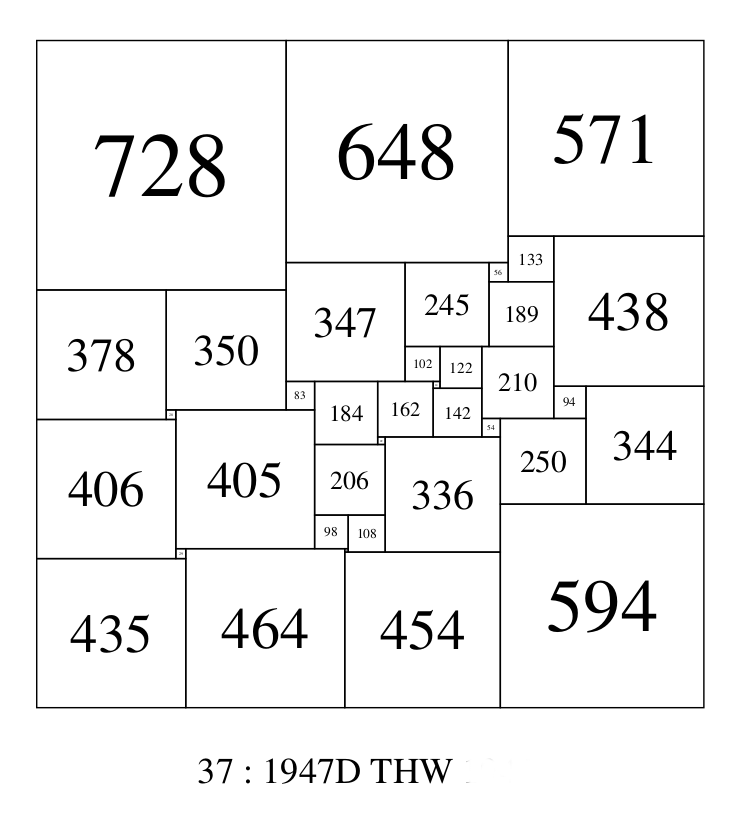
- T. H. Willcocks, Some Squared Squares and Rectangles, Journal of Combinatorial Theory 3, 54-56 (1967) .
- C. J. Bouwkamp and A.J.W. Duijvestijn, Album of Simple Perfect Squared Squares of order 26, EDT Report 94-WSK-02 Eindhoven, July 1994, vi-vii.
- G. H. Morley, private correspondence 2013, 2014.
- Martin Gardner; The addendum (pp. 162-4) to Tutte's chapter in Martin Gardner's More Mathematical Puzzles and Diversions (1961) "The smallest published square that is both simple and perfect is a 38th-order square with a side of 4,920, discovered by R.L. Brooks. In 1959 this was bettered by T.H. Willcocks of Bristol, with a 37th-order square, 1,947 on the side."
- W. T. Tutte, Squaring the Square, Canad. J. Math. 2 (1950).
- I. Gambini, Thesis (1999) Quant aux carrés carrelés.