'Special' Perfect Squared Squares

'Special' Perfect Squared Squares are Perfect Squared Squares, (PSSs ie CPSSs and SPSSs) which have some features or property which makes them 'special'.

Among the characteristics which mark PSSs as being 'special' are items in the following list;

• Lowest Order PSS (Perfect Squared Square)

  For many years the lowest order PSS was the 'Holy Grail' of squared square research. The lowest order PSS was discovered in a computer search by Duijvestijn in 1978. By 'lowest order' we mean the squared square with the fewest squares. The 'order' is the number of squares in the dissection. The squared square must be 'perfect', that is, no two squares are the same size.

  

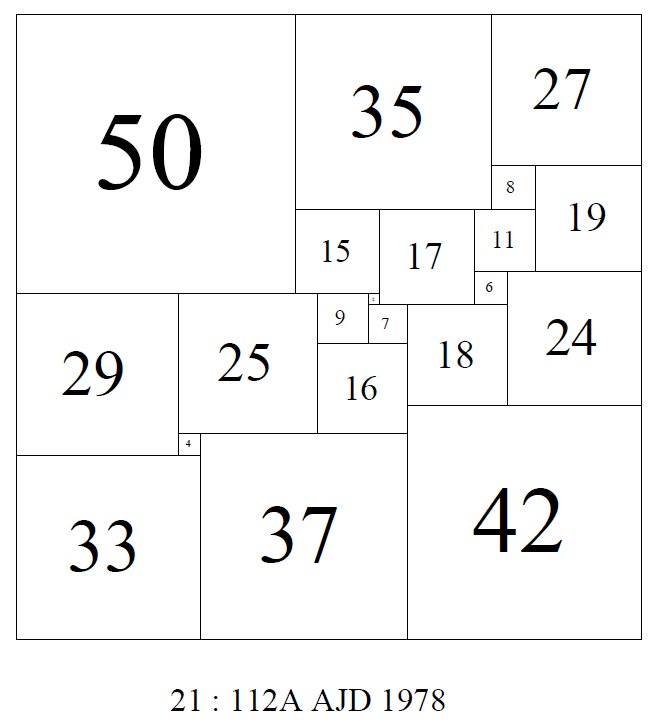
  Duijvestijn's order 21 SPSS (simple perfect squared square) is unique, it is the only SPSS of order 21, and order 21 is the only PSS order with a count of one. A common misconception about the lowest order PSS is that it is also the smallest PSS. It is not. Duijvestijn's order 21 SPSS has a side of 112. There are SPSS of higher order, but which have a smaller side than 112. They are the next entry in our list of Special Squared Squares.

• Smallest size PSS

  The smallest PSS size is 110. There are 3 SPSSs with a side of 110.

  

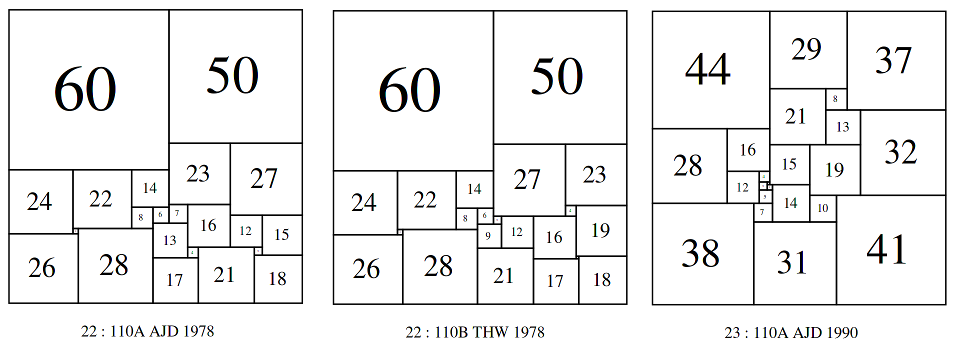
  Bouwkamp wrote in 'Catalogue of Simple Perfect Squared Squares of orders 21 through 25'

  "The very first Simple Perfect Squared Square of this Catalogue was discovered by computer in March, 1978, by Duijvestijn. It has the lowest possible order, n = 21, and it is the only one of that order. In July of the same year, Duijvestijn found two simple perfect squared squares of order 22. After communicating these to P.J. Federico of Washington, D.C., U.S.A., who informed T.H. Willcocks of Bristol, U.K., the latter found a third simple perfect squared square of order 22 about August 1978."

  Later, in 'Album of Simple Perfect Squared Squares of order 26 by C.J. Bouwkamp and A.J.W. Duijvestijn' Bouwkamp gave some more intriguing details of the discovery of the Willcocks 110;

  "These two squares were sent to Federico, who in turn communicated them to Willcocks. When Willcocks studied 22:110, in trying to find the rectangular generators of the square in the sense of Wilson, he "was listening to the broadcast news and my mind was less than half on this problem so, in error ... found '" a second square" and he continues "This goes to show that even stupidity may sometimes yield a useful result". That is Willcocks's story of the birth of 22:110 by serendipity. It is a pity that details of Willcocks's analysis have not appeared in print."

  The third SPSS with size 110, or order 23 was discovered some years later, Bouwkamp again;

  "Then, in 1990, Duijvestijn decided to start all over again when computer power had tremendously grown compared to that of the sixties. He first found eight simple perfect squared squares of order 22, including his earlier two. Secondly, he found twelve of order 23 and twenty six of order 24."

  Among the twelve order 23 SPSSs was another with a side of 110.

  How do we know these three 110 size PSSs are smallest? This is an interesting question, considering the existence of these 3 110 SPSSs (2x 22:110 and 23:110), alongside the 21:112 SPSS, shows that perfect squared squares at a higher order can have a smaller size than those at a lower order. There are several proofs that these are the smallest PSSs. Before we go to the proofs, it is instructive to eliminate some other possibilities which were thought to be possible candidates for the smallest perfect squared square. One of these was based on the curious fact that 1²+2²+3²+...+24² = 70². We can show this is true using the sum of squares formula for the first n integers and making it equivalent to a square number, i.e. S² = n(n + 1)(2n + 1)/6. Solutions to the formula n(n + 1)(2n + 1)/6 are the pyramidal numbers. The first few pyramidal numbers are: 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819 (sequence A000330 in OEIS). Solving the diophantine equation, S² = n(n + 1)(2n + 1)/6 involves finding a pyramidal number which is also a square number, this is a known problem, the Cannonball Problem, and was solved in 1918 by Watson. The only solutions in integers for (n,S) are (1,1) and (24,70). The trivial solution (1,1) corresponds to the unit square, and it was conjectured that the squares 1 to 24 might tile a square of size 70. If this were true there would exist a perfect squared square (PSS) of size 70. However Martin Gardner wrote in his book Mathematical Carnival, that in 1974 two computer scientists at the University of Illinois at Urbana-Champaign, Edward M. Reingold and James Bitner, wrote a program to solve this problem and with it they proved that such a tiling was not possible.

  Another possible candidate for the smallest perfect squared square was thought to be T.H. Willcocks 1948 discovery of the order 24, side 175 compound perfect squared square (CPSS). This is the lowest order and smallest size CPSS, and held the record for the smallest PSS for thirty years, but the discovery of the size 110 SPSSs shows it is not the lowest order and smallest size PSS.

  In 1999 Ian Gambini presented his thesis (French) and proved, using a tiling decomposition algorithm, that the smallest perfect squared square is 110 in size, and that there are three distinct solutions (ignoring symmetries). See "A method for cutting squares into distinct squares", Ian Gambini, Discrete Applied Mathematics 98 (1999) 65–80 for an English translation featuring this result.

  Despite the negative result for tiling 70² we can use the equation S² = n(n + 1)(2n + 1)/6, to get lower bounds on the size of a PSS by order. For a PSS to be as small as possible we need to minimise the size of the squares in the dissection, and minimise the difference in sizes between squares, while ensuring that none of them are the same size. This can be done by using consecutive integers starting at 1. No PSS could be smaller in size than the square root of the sum of the square of the first n integers where n is the order, because consecutive integers have the smallest difference (a difference of 1) between successive integers, and consecutive integers starting at 1 are the smallest possible set of n integers in sizes from a set of all possible n integers. We can use the sum of squares formula to find the 33rd pyramidal number (or just sum the squares of the first 33 integers), it is 12529. The square root of 12529 is approximately 111.93. So a PSS with a side less than 112 could not have more than 32 squares. Conversely if any PSSs with less than a side of 112 exist, they could only exist in orders 21 to 32. (Duijvestijn proved that no PSSs exist below order 21, and this fact has been confirmed many times since). As of September 2013 PSSs of orders 21 to 32 were completely enumerated by Lorenz Milla and Stuart Anderson and the smallest PSSs found were the 3 known SPSSs with a size of 110. This provides another proof of Gambini's result that 110 is the smallest possible size for a PSS.

• Smallest Size PSS per Order

  PSSs can be compared to each other by comparing sizes. PSS of the same order have a characteristic size distribution. If one is comparing sizes of PSSs across different orders, one may wish to take the order into account. A simple way of comparing the size of PSSs while adjusting for the order is just to divide the size of a PSS by it's order. Using this size/order measure PSSs of different orders can be compared according to how they are situated relative to the size distribution in their own order. However the comparison only seems to work for the smaller PSSs in each order. The smallest possible SPSSs of each order from 21 to 32 are 112, 110, 110, 120, 147, 212, 180, 201, 221, 201, 215, 185. (This is OEIS sequence A217148 - and appears to be the same sequence as A129947). These are also the smallest PSSs of these orders. Based on James Williams work the best known values for orders 33 to 39 are; 246, 315, 276, 341, 319, 352, 360. These terms have a size/order measure ranging from 4.782 for the 23:110 SPSS, 5 for the two 22:110s and 24:120, up to 9.47 for 36:341. By this measure 23:110 is both the smallest known PSS in relative terms by size/order and in absolute terms by size. A pdf of the SPSS dissections for A129947 is here.

• Largest Size PSS by Order

  As the order increases, the sizes that are possible for PSS increase also. Unlike the smallest PSS, there is no bound on the largest size for a PSS. However as the number of PSS in a given order are finite, there is always going to be a largest size for any particular order. The largest possible PSSs of each order from 21 to 32 are; 112, 192, 332, 479, 661, 825, 1179, 1544, 2134, 2710, 3641, 4988. They are all SPSSs. This is OEIS sequence A217149. A pdf of the SPSS dissections for A217149 is here.

• Maximum Element Size by Order

  The largest possible elements of each order of PSS from 21 to 32 are; 50, 97, 134, 200, 343, 440, 590, 797, 1045, 1435, 1855, 2505. They are all SPSSs. This is OEIS sequence A228953. A pdf of the SPSS dissections for A228953 is here.

• Maximum Element Size as a Proportion of the PSS Size

  How large can an element be as a proportion of the PSS size? Among the complete orders 21 to 32 the best is an element a little over 2/3rds (66.7%) of the size of the PSS. This pdf has the best result in each order from 21 to 32.

  We can do much better, it should be possible to construct CPSSs so that the largest element approaches 100% of the size of the CPSS. The trick is to create 2 long thin, simple perfect squared rectangles (SPSRs) with particular ratios and then add an large extra square in the remaining space. For example Brian Trial has created 1xn SPSRs from n = 4 to 18. Creating 1xn SPSRs is a natural generalisation of the squared square problem (which is 1xn, n=1) and is quite difficult to do. Brian's results on this problem are extraordinary.

  Two pdfs of Brian's 1xn SPSRs are here;
  (landscape version) and (portrait version). By scaling and fitting Brian's 1x17 and 1x18 SPSRs and adding one extra square, equal to the size of the long side of the scaled 1x17 rectangle, a compound perfect squared square (CPSS) is created with the largest element square having a side equal to 94% of the CPSS side. A pdf of this CPSS (order 560; size 338321736) has been constructed. The elements are dwarfed by the larger square, you need to zoom in to see the smaller elements along the sides.

• Crossed PSSs

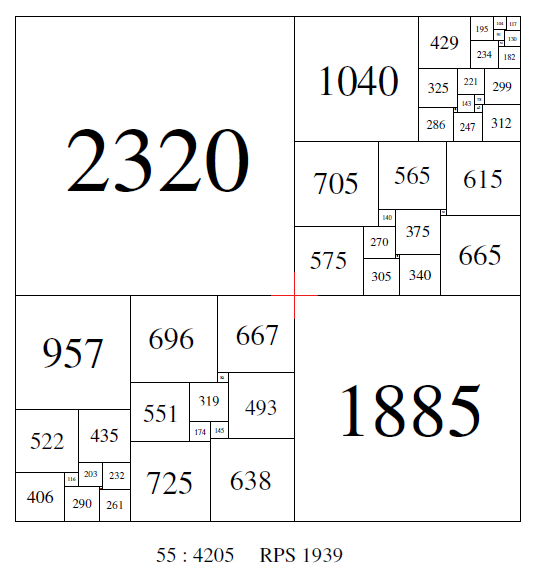
  Some the earliest known perfect squared squares featured crosses in their construction. For example, Sprague's square of order 55, side 4205.

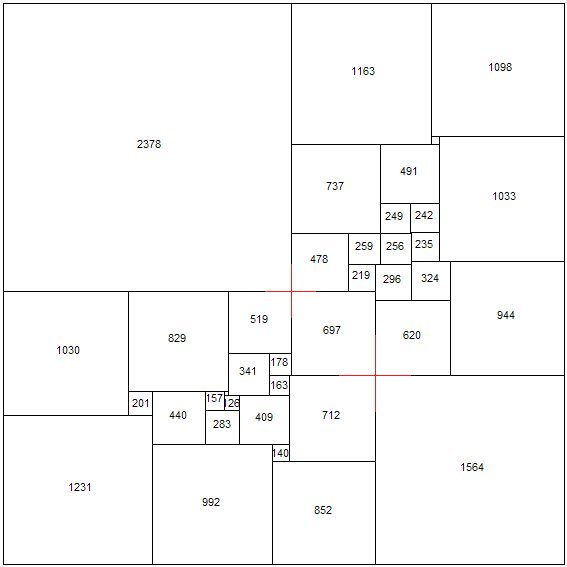
  A compound perfect squared square found by Roland Brooks, using the rotor-stator symmetry method, has 2 crosses;

  A compound perfect squared square found by Arthur Stone, using 2 order 13 simple perfect squared rectangles, and 2 additional squares, has a cross. This is the R1, R2 Moron construction and is a crossed construction;

  

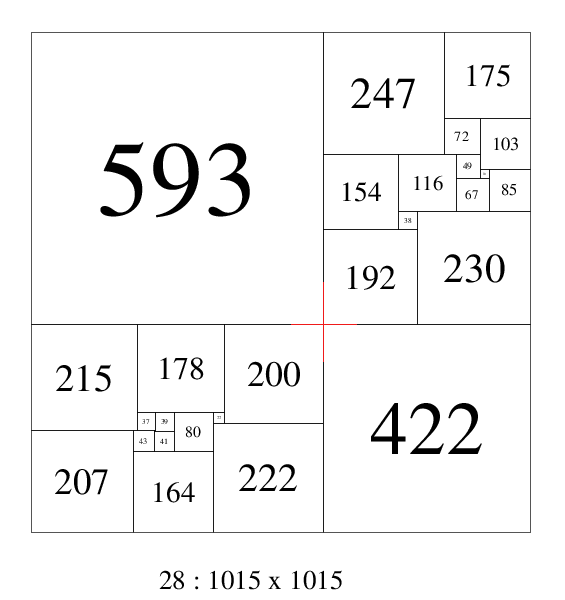
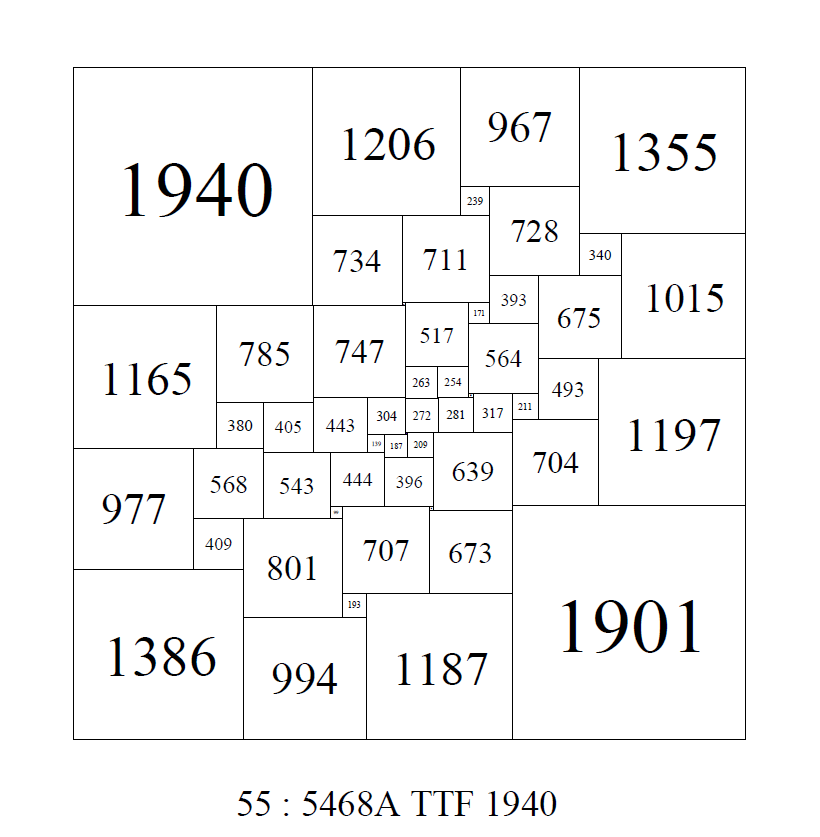
  In Brooks, Smith, Stone, Tuttes 1940 paper "The Dissection of Rectangles into Squares" they referred to an order 55 SPSS created using advanced rotor stator techniques.  The square had no cross and this was regarded as an achievement.  The cross being regarded as a 'blemish', indicative of the construction, which should be eliminated  where possible, although it was quickly realised that Perfect Squared Squares with crosses were quite a rare phenomena.

  Duijvestijn recorded the bouwkampcode and the orders in which crosses first appeared.  In order 26 he found the first SPSS with a cross of lowest order[1]. He also found the lowest order CPSS with a cross in order 26. With CPSSs one needs to examine all the isomers of a CPSS, as some isomers may be crossed, and other isomers of the same CPSS are not. The lowest order SPSR and SISR with a cross are in order 17 and and the lowest order SISS with a cross is in order 18.   I have extended the counts a little further to order 20 for squared rectangles and order 28 for squared squares.
  

  
  

  THE NUMBERS OF CROSSED SQUARED RECTANGLES AND SQUARED SQUARES
  

  Order	SPSR	SISR	SPSS	CPSS	SISS	CPSR
  9	-	-	-	-	-	-
  10	-	-	-	-	-	-
  11	-	-	-	-	-	-
  12	-	-	-	-	-
  13	-	-	-	-	-
  14	-	-	-	-	-
  15	-	-	-	-	-
  16	-	-	-	-	-
  17	2	5	-	-	-
  18	2	8	-	-	2
  19	7	36	-	-	-
  20	29	72	-	-	10
  21	166		-	-	4
  22			-	-	58
  23			-	-	57
  24			-	-	366
  25			-	-	351
  26			1	1	1858
  27			3	-	1998
  28			10
  29			23
  30			71
  31			146
  32			338

• isomers (PSSs of same size, all elements pairwise the same, arranged differently) - [all CPSSs exist as isomers, generally only SPSS isomers are considered special]
• disjoint n-tuples (PSSs of same size, all elements pairwise different, arranged differently) - [in higher orders disjoint n-tuples of the same size are the rule, not the exception, so these are only 'special' in lower orders]
• 'nice' PSSs (PSSs where we minimise the difference in size between the smallest and largest element (or side length))
• maximum number of largest elements not in corner (or boundary)
• minimum number of boundary elements in a PSS (7)
• maximum number of boundary elements in a PSS (>50%)
• minimum size (5) of boundary element in a PSS
• minimum corner element size in a PSS
• maximum number of prime elements in a PSS (>50%)
• minimum number of prime elements in a PSS (0)
• minimum number of even elements in a PSS
• element situated at the center of a PSS