Squared Tori

A torus and the gluing instructions to create a torus from a square.
Topologically, the torus can be defined as the fundamental square [0,1] × [0,1] with its top and bottom sides identified by the relation (x, 0) ~ (x, 0) for 0 ≤ x ≤ 1, and left and right sides identified by the relation (0, y) ~ (0, y) for 0 ≤ y ≤ 1 as in the diagram on the right. To put it another way, it can be constructed from a rectangle by gluing both pairs of opposite edges together with no twists.
An (ordinary) torus is a surface having genus one, and therefore possessing a single "hole". The usual torus embedded in three-dimensional space is shaped like a donut.
Squaring the Torus
Squaring the torus was mentioned as a generalisation of the squaring the square problem in the 1940 paper by Brooks, Smith, Stone and Tutte [7]. However the electrical method of the 1940 paper worked only where the current entered at one node and exited at another [8]. In 1999 Ian Gambini found a solution to the problem of squaring the torus [3]. He found a 181 x 181 simple perfect squared square torus of order 24. This is the only known example of a simple perfect squared (square) torus. Interestingly, the determinant of the electrical network graph of Gambini's simple perfect squared torus factorises in the same manner as does the determinant of a squared square network graph. Gambini also gave several examples of simple perfect squared rectangle tori.
In more recent times Geoffrey Morley has attacked the problem. What follows are some of his constructions and notes for a 2014 talk on "Squaring The Torus" at MathsJam.
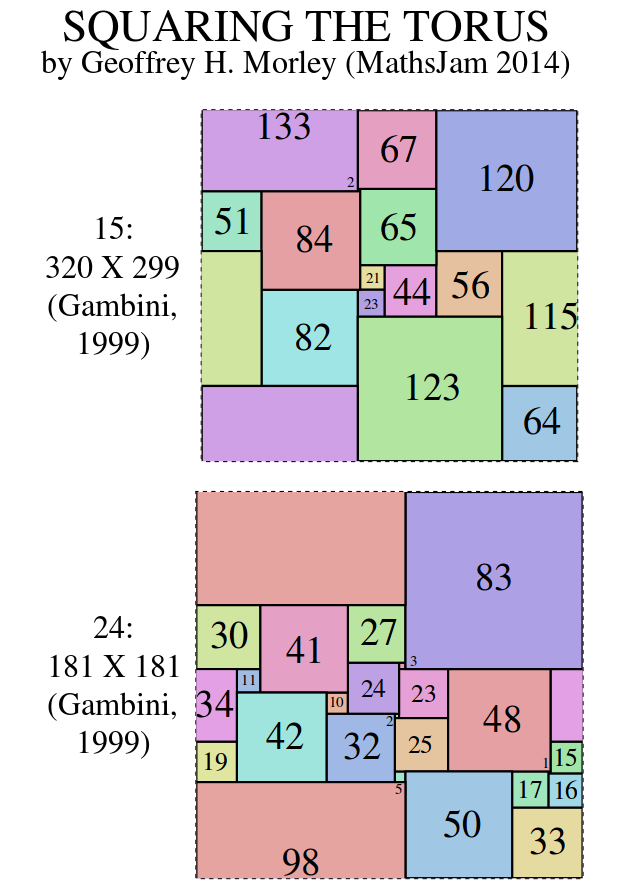
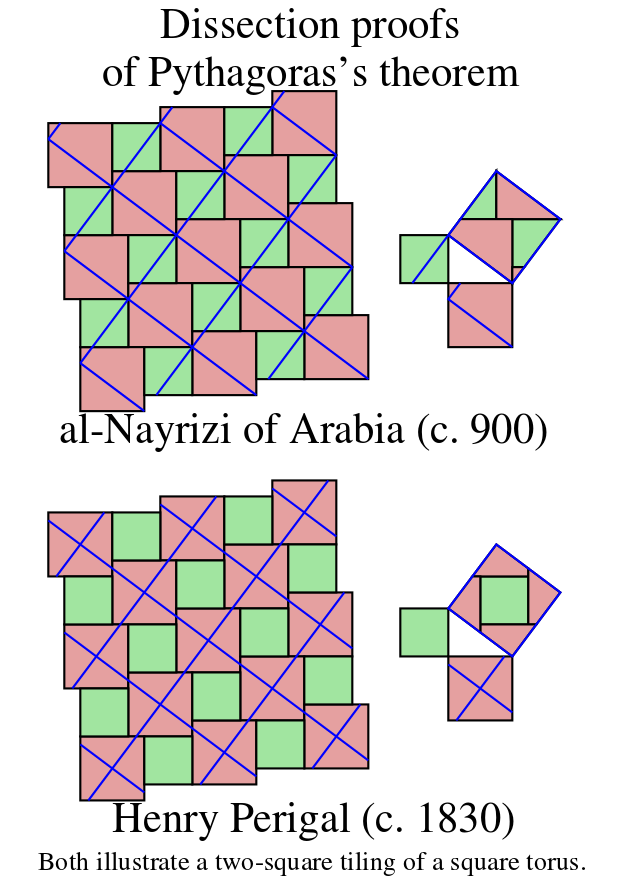
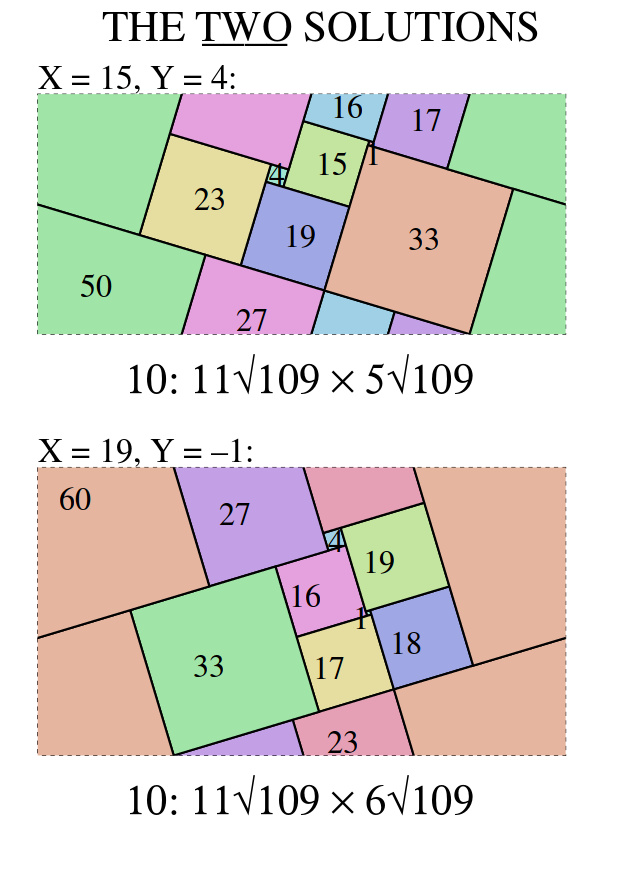
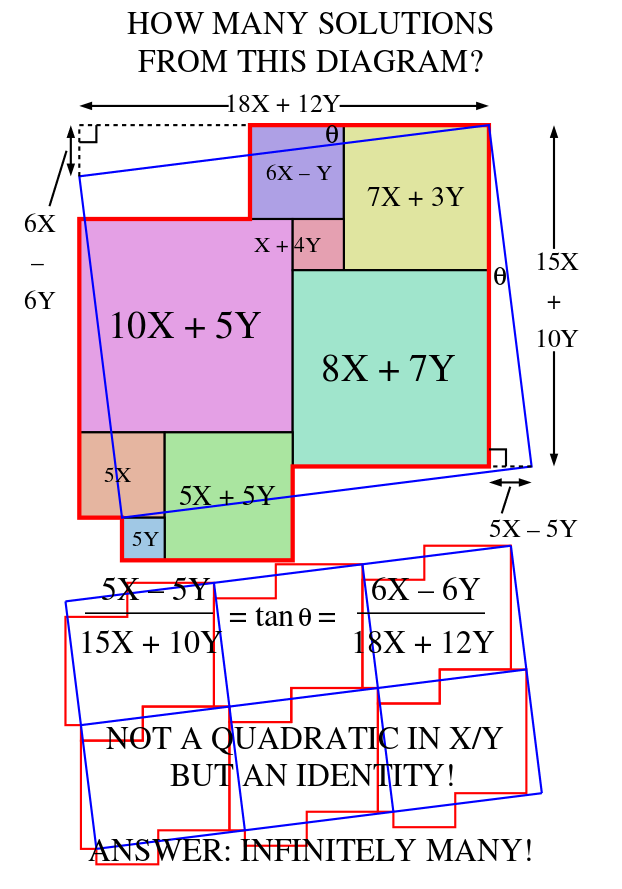

The attached pdf file (or postscript file) has the Perfect Squared Tori with integer-sides listed below.
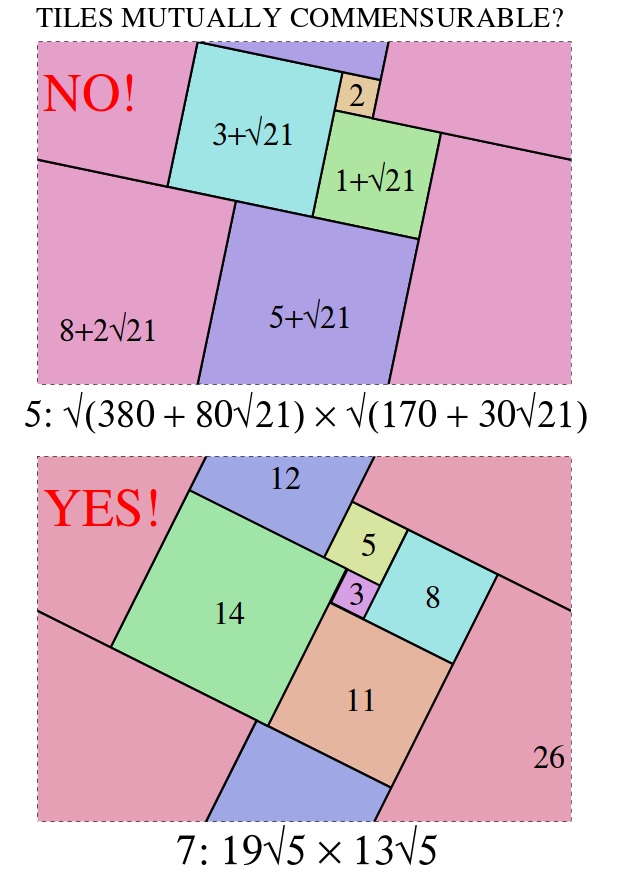
Most squared tori with tile sides not parallel to the sides of the rectangle do not have commensurable tile sides. How should noncommensurable tile sides be scaled? I suggest each tile side be a+b√c where a, b and c are integers, c is squarefree, and b=0 for the smallest square. And of course the a's and b's should have no common factor. But usually I'm interested only in squarings with commensurable tile sides.
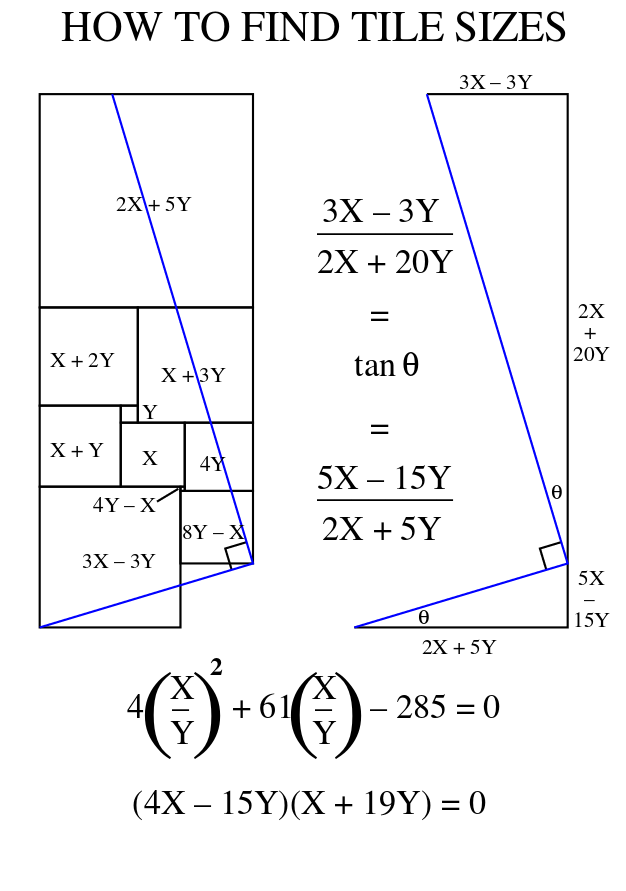
Each lattice cell is a√c X b√c where a, b, and c are integers, and c is squarefree. For each order, squarings are ordered according to the values of c, a, and b. a/b has the same value for all instances of a continuously deformable squaring. There are now three known nondeformable examples (all of order 11) with c=1.
- Each catalogued squaring is either nondeformable and crossfree or labelled with one of the following properties:
- * = smallest crossfree instance with integer dimensions (c=1) of a deformable squaring;
- z = crossed instance of a deformable squaring in which one square, not counted in the order, has shrunk to a point (that is, has zero side length).
Any instance of a deformable squaring is obtainable by substituting appropriate values for x and y in the variable side lengths.
List of Perfect Squared Tori with Integer-Sided Tiles by Geoffrey Morley.
Remove the nonsquare rectangular tile(s) from the rectangle dissection described in Bouwkamp code. Tile the plane with translations of the polygon that remains. Draw lattice lines that intersect at right angles, for example at the centre of each instance of the largest square.
Order 2
- *2: 5 X 5: (4,3)(3x1).
Order 7
- 7: 19√5 X 13√5: (26,14,11)(3,8)(12,5)(13x7).
Order 8
- *8: 78 X 65: (41,31,25x33)(29,2)(27)(22,19)(3,72x3).
- *8: 150 X 125: (79x3,55,45)(79)(10,35x75)(65)(41,38)(3,135x3).
- 8: 34√5 X 31√5: (41,21,34x10)(11,23)(20,12)(35)(34x27)(27).
Order 9
- 9: 32√5 X 19√5: (38,32x45)(26,12)(5,8,19)(14,3)(11).
- z9: 11√34 X 10√34: (34,16,33x4)(12,21)(19,9)(30)(33x21,1)(20).
Order 10
- *10: 55 X 50: (29,12,33x6)(6,27)(18)(11,17,1)(16,3)(30x13)(11x6).
- *10: 130 X 117: (65,55,45x15)(32,13x43)(8,24)(10,53)(13)(32x43,43)(37).
- *10: 143 X 65: (60,31,41x8,25x5)(3,22)(25,19)(41)(29,2)(27)(116x8).
- *10: 143 X 78: (72,60x41)(31,29)(2,27)(42x41,41,22)(19,3)(30)(102x14).
- 10: 65√2 X 35√2: (49,26,16x13)(16)(23,3)(19)(5,14)(68x13,4)(9).
- 10: 49√5 X 47√5: (53,45,47x45),20,23,49)(41,12)(29,3)(26).
- 10: 65√5 X 31√5: (114x1,12,35)(62,41,11)(23)(27,31)(21,20)(47x4)(83x3).
- 10: 32√29 X 27√29: (76,74,64)(10,54x71)(2,21,61)(59,19)(40).
- 10: 61√53 X 32√53: (224,101,102,64x102)(56,45)(44,122)(11,78)(67).
Order 11
- 11: 104 X 65: (60,21,40)(11,10)(1,9)(12)(4,20,25x20)(16).
- 11: 299 X 169: (156,70,115)(39,31)(8,23)(47)(9,41,65x41)(32).
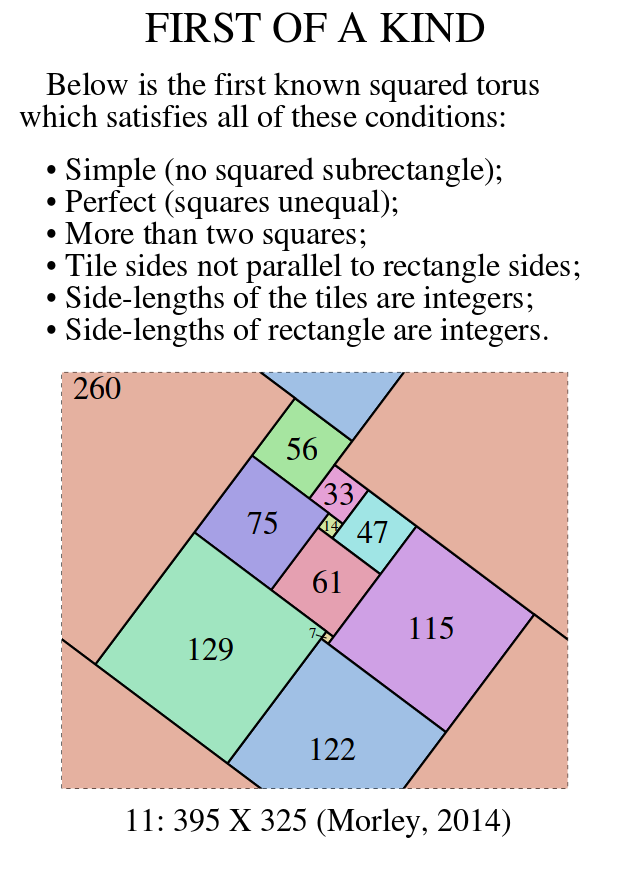
- 11: 395 X 325: (260,129,122)(7,115)(75,61)(14,47)(56,33)(195x23).
- 11: 51√5 X 32√5: (64,38,32x13)(32)(26,12)(5,8,19)(14,3)(11).
- 11: 51√5 X 49√5: (49,47,25,28)(22,3)(31)(2,55,12)(51x53)(43).
- 11: 56√5 X 34√5: (51,17,56x17)(34,39)(56x61,24,5)(19,25)(37,6)(31).
- 11: 79√17 X 49√17: (196,120,49x117)(17,32)(76,30,14)(16,15)(47)(46).
- 11: 167√17 X 152√17: (368,300,152x397)(68,135,97)(196,240)(38,211)(173)(152x44,44).
- 11: 17√29 X 16√29: (52,30,32)(28,2)(34x53)(33,13,6)(7,27)(20).
- 11: 21√34 X 11√34: (55,33,50x12)(20,30)(1,19)(34)(9,21)(16,12)(55x12)(33x4).
- 11: 16√41 X 9√41: (45,64x43)(13,14,37)(34,11)(23,1)(15)(7,8)(64x1).
- 11: 61√61 X 48√61: (240,202,124,27x126)(91,31,2)(29)(60)(38,164)(151)(278x126).
- 11: 53√74 X 37√74: (259,141,156)(118,23)(8,39,109)(31)(70)(371x6,6).
- 11: 17√82 X 15√82: (80x4,73)(80)(11,62)(36,55)(17,19)(4,58x17)(15,2)(80x13).
- 11: 5√106 X 4√106 A: (25,21,19)(2,17)(8,15)(20x11,5)(1,7)(6).
- z11: 5√106 X 4√106 B: (117,49,43)(6,37)(24,31)(17,7)(10,65x37)(27).
- 11: 16√106 X 13√106: (19x29,22,20)(14,6x29)(10,12)(16,3)(13)(11,15)(36x4,4).
- z11: 17√109 X 16√109: (91,79,51)(51x91)(31,48)(3x69,69,19)(50)(33,15)(18,48x18).
- 11: 5√130 X 3√130: (33,16,15)(6,9x18)(7,4,5)(3,1)(12)(10).
- 11: 7√130 X 5√130: (55,22,15x37)(10,12)(7,3)(1,5,21)(4)(16).
- 11: 13√130 X 7√130: (77,48,39)(18,21x38)(29,12,7)(5,2)(20)(17).
- 11: 19√130 X 13√130: (143,66,39x86)(29,17,20)(12,5)(2,57)(7)(48).
- 11: 8√145 X 5√145: (60,21,15x8)(15)(19,2)(17)(20,16)(4,12)(76x8)(8).
References
- Anderson, S. E. & Morley, G. H., Faultfree Perfect Squared Klein Bottles (FPSKBs).
- Anderson, S. E. & Morley, G. H., Faultfree Perfect Squared Projective Planes (FPSPPs).
- Gambini, Ian (Dec. 1999), Quant aux carrés carrelés. PhD thesis, L'Université de la Méditerranée aix-Marseille II) (Especially pp. 81-85.) [In French]
- Morley, G. H. (Jan. 2014), Perfect squared Klein bottle myths, MathsJam 2013 talk notes.
- Nelsen, Roger B. (Nov. 2003), Paintings, Plane Tilings, & Proofs, Math Horizons, MAA, 5-8. Reprinted in Haunsperger, Deanna; Kennedy, Stephen (2007), The Edge of the Universe: Celebrating Ten Years of Math Horizons, Spectrum Series, MAA, 295-298.
- Perigal, Henry (1872), On Geometric Dissections and Transformations, The Messenger of Mathematics (second series) vol. 1, pp. 103-106. [Apparently 1872, not 1874.]
- R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T. Tutte, 'The dissection of rectangles into squares'. Duke Math. J. 7 (1940) 312–340.
- R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T. Tutte, 'Determinants and current flows in electric networks', Discrete Math. 100 (1992) Special volume to mark the centennial of Julius Petersen's "Die Theorie der regularen Graphen", Part I, 291-301.
- Donald Knuth - "Finding All Spanning Trees" . See his programs for GRAYSPAN, SPSPAN, GRAYSPSPAN, and a MetaPost source file for SPSPAN, plus an auxiliary program SPGRAPH. Three instructive ways to generate all spanning trees of a graph. (August 2003)