Faultfree Perfect Squared Klein Bottles (FPSKBs)

A 2D representation of the Klein bottle
immersed in 3D space
In mathematics, the Klein Bottle is an example of a compact non-orientable two-dimensional manifold. It is a one-sided surface. Other related non-orientable objects include the Möbius strip and the real projective plane Whereas a Möbius strip is a surface with boundary, a Klein bottle has no boundary (for comparison, a sphere is an orientable surface with no boundary)[1].
The Klein bottle was first described in 1882 by the German mathematician Felix Klein.
To construct a Klein Bottle, start with a square, and then glue together corresponding coloured edges, in the following diagram, so that the arrows match. More formally, the Klein bottle is the quotient space described as the square [0,1] × [0,1] with sides identified by the relations (0, y) ~ (1, y) for 0 ≤ y ≤ 1 and (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1:
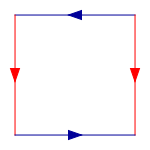
Gluing opposite edges of
a square to create a Klein bottle.
This square is a fundamental polygon of the Klein bottle.
Note that this is an "abstract" gluing in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle. The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions.
Glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends together so that the arrows on the circles match, pass one end through the side of the cylinder. Note that this creates a circle of self-intersection. This is an immersion of the Klein bottle in three dimensions.
A Klein bottle can also be studied by imagining it to be the result of identifying (or gluing) the two vertical edges of a rectangle, and its two horizontal edges but in opposite directions. That is the way all the squared Klein bottles depicted on this site are oriented.
We are interested in dissecting the surface of the fundamental polygon when it is a square, (or rectangle with the same gluing instructions), into a finite number of smaller squares, called the elements. As a Klein bottle has no boundary, the edges of the square elements of the dissection can be parallel with edges of the fundamental polygon, but need not coincide with them, or the edges of the square elements can be at 45 degrees to the rectangle sides. If the edges of elements and fundamental polygon are parallel then the elements are commensurate with the rectangle edge sizes, alternatively, if they are at 45 degrees then the rectangle edges are multiples of √2.
In both cases the sizes of the elements are commensurate with each other and can be expressed as integers divided by any common factor. If the sizes of the elements dissecting a Klein bottle are all distinct, (no two the same size), then we call the dissection perfect. The number of elements in the dissection is called the order. We call a tiling faultfree if has no fault line, which is what we call a glued edge that does not intersect any tiles. We use the abbreviation FPSKB for Faultfree Perfect Squared Klein Bottle.
Only five known FPSKBs below order 8 (two of order 6 and three of order 7) have tile sides parallel to the sides of the rectangle. The only other type of FPSKB, and by far the most common, has tile sides at 45 degrees to the sides of the rectangle.
A squared polygon can sometimes be glued to construct both an a√2 x b/√2 FPSKB and a b√2 x a/√2 FPSKB. Here are the known pairs of values of a and b for orders 4-7:
- Order 4 hexagon: (5,6).
- Order 5 hexagons: (5,11), (8,11).
- Order 6 hexagons: (8,19), (13,16), (13,19) twice.
- Order 6 octagon: (13,22).
- Order 7 hexagons: (13,29), (13,32) twice, (19,32) twice, (21,32) twice, (24,27), (24,29).
- Order 7 octagons: (13,35), (19,37) twice, (21,35), (21,38).
Every one of the known 28 FPSKBs of order 7 that has a sloping tile with side 12, 15 or 18 also has a tile with side 8. There is probably no significance in this, but no other square with side < 21 has an ever-present companion.
All of these Klein bottle dissections have been discovered recently by Geoffrey Morley and assembled by him into this collection. Geoffrey has also authored some postscript programming code which is the basis for the dissection graphics on this page.
The dissections are available as a pdf file and a postscript file. This is currently an active area of research, new dissections are being discovered, making the current illustrations incomplete and out of date. These will be updated when the rate of discovery slows down.