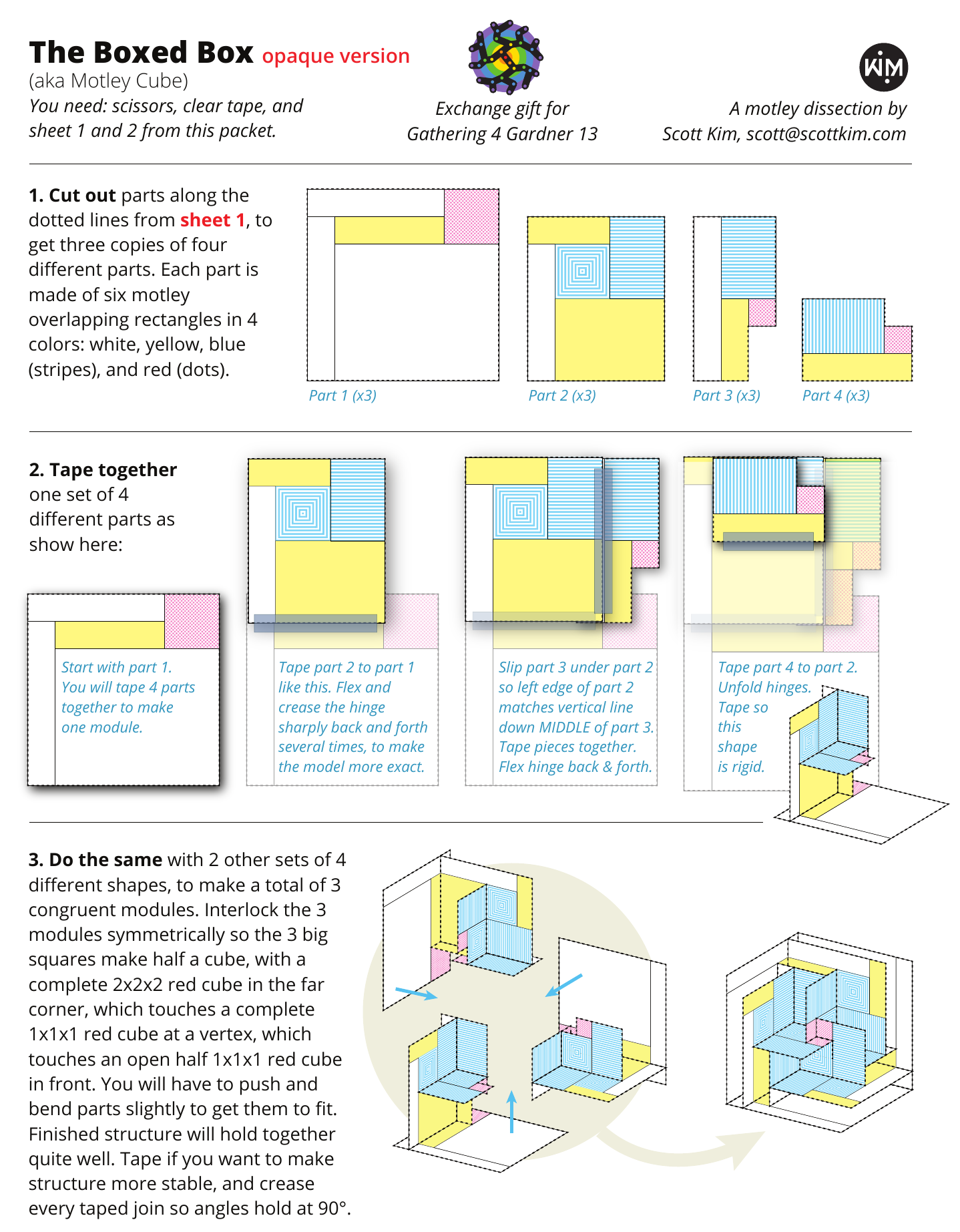
Motley Dissections
Scott Kim, June 30, 2018 • For Gathering 4 Gardner 13
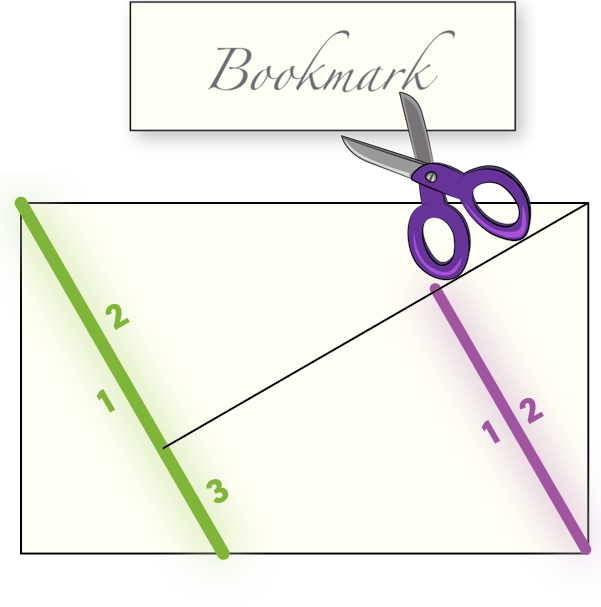
The cut-up bookmark. When I was in sixth grade my teacher handed out blank cards and asked us to make bookmarks. I decided to cut mine up. I challenged myself to make a hard puzzle that had just a few simple pieces.
First attempt. Here’s the puzzle I made. It has just four simple pieces and is decently hard to solve. And by happy accident there are two ways to make a rectangle with these pieces. Notice that the green line is borders one piece on one side, and two pieces on the other side. This sort of edge makes the puzzle harder to solve, since you can’t find which piece goes with which just by matching edges of the same length. But along the purple edge, two pieces do share a complete edge. I wondered: can one make a dissection where no two pieces share a complete edge?
The squared square. The answer is yes, and such constructions are called “motley dissections,” a term coined by computer scientist Donald Knuth. The most famous motley dissection is the squared square — a square cut into squares all of different sizes. At left is the smallest possible squared square, confirmed by computers search, which contains 21 squares. No two squares here completely share an edge, because if they did, the squares would be the same size. Martin Gardner wrote about the squared square, first discovered by graph theorist William Tutte and others, in his Scientific American column [1].
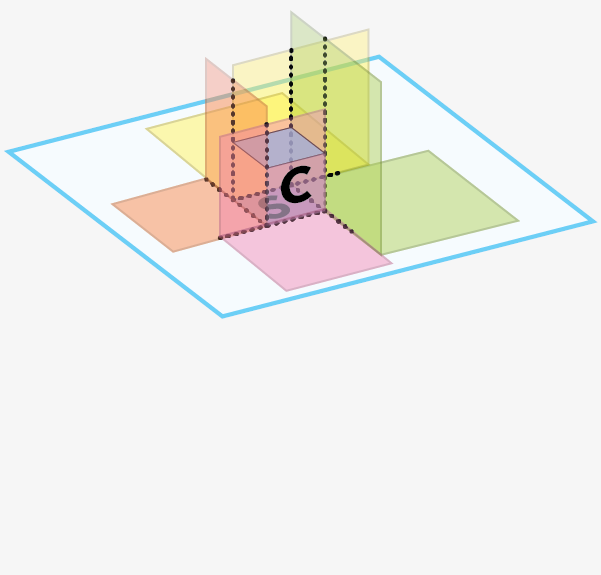
No cubed cube. If a squared square is possible, what about a cubed cube? Impossible, unfortunately. Here is the proof from Gardner’s column. Assume it is possible to cube a cube. The ground floor must be a squared square. Within that square there must be a smallest square S. We know that S cannot touch the outer edge of the base square, because then the neighboring squares, which are all larger than S, would overlap. Therefore, S must be in the interior of the base, where the cube C with base S is surrounded on all sides by larger, taller cubes. But that means that the top surface of C must be a smaller squared square, because cubes that rest on the top surface of C cannot extend beyond its edges. This logic creates an infinite sequence of smaller and smaller cubes. Therefore, a cube cannot be cut into a finite number of cubes, all of different sizes.
Polygons
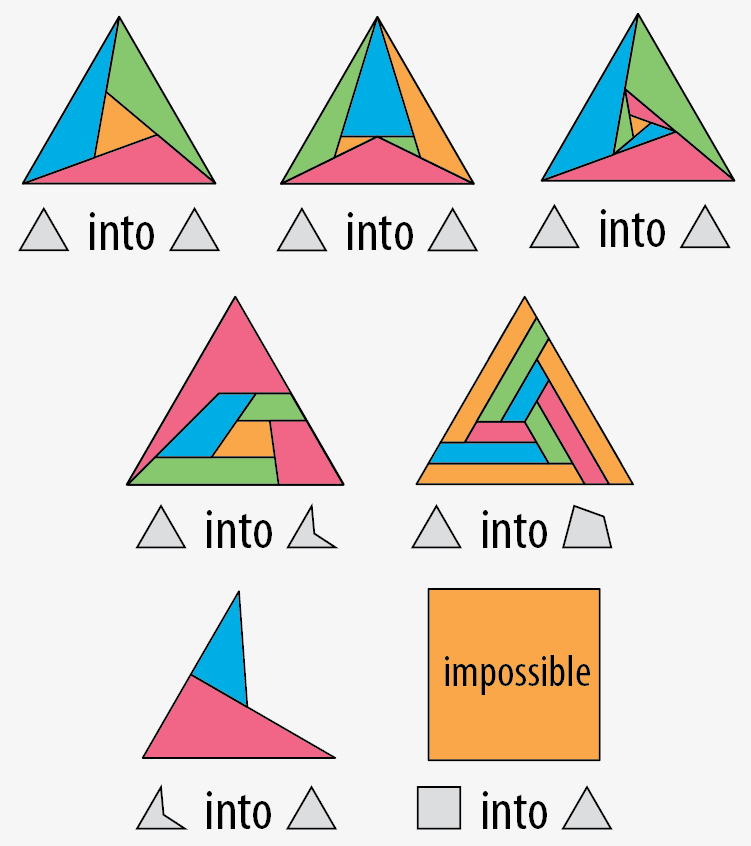
What other shapes can be cut up as motley dissections? Let’s try other polygons.
Triangles. You can cut a triangle into motley triangles. You can do it with four triangles. Six triangles. Seven triangles. Or more. You can cut a triangle into six quadrilaterals. You can cut a triangle into nine convex quadrilaterals. (Proof pending that this is minimal.) You cannot cut a convex quadrilateral into triangles, unless you use infinitely many (proof pending). The proof involves counting the number of edges, concave angles, and “receptive” edges in the perimeter polygon — a receptive edge” is one that is already shared by two other polygons, and thus can receive another polygon along its full exposed length without violating the motley condition. The two red edges in the concave quadrilateral are both receptive; the other two edges are not.
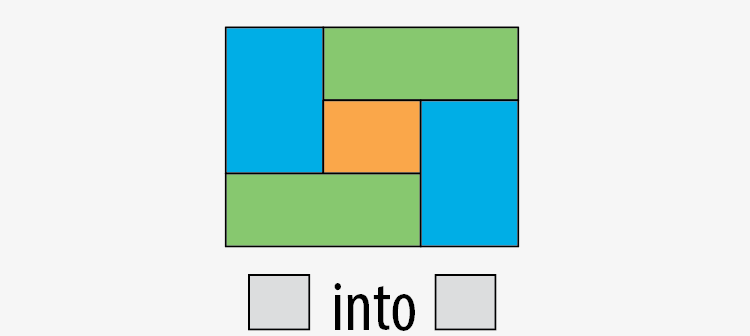
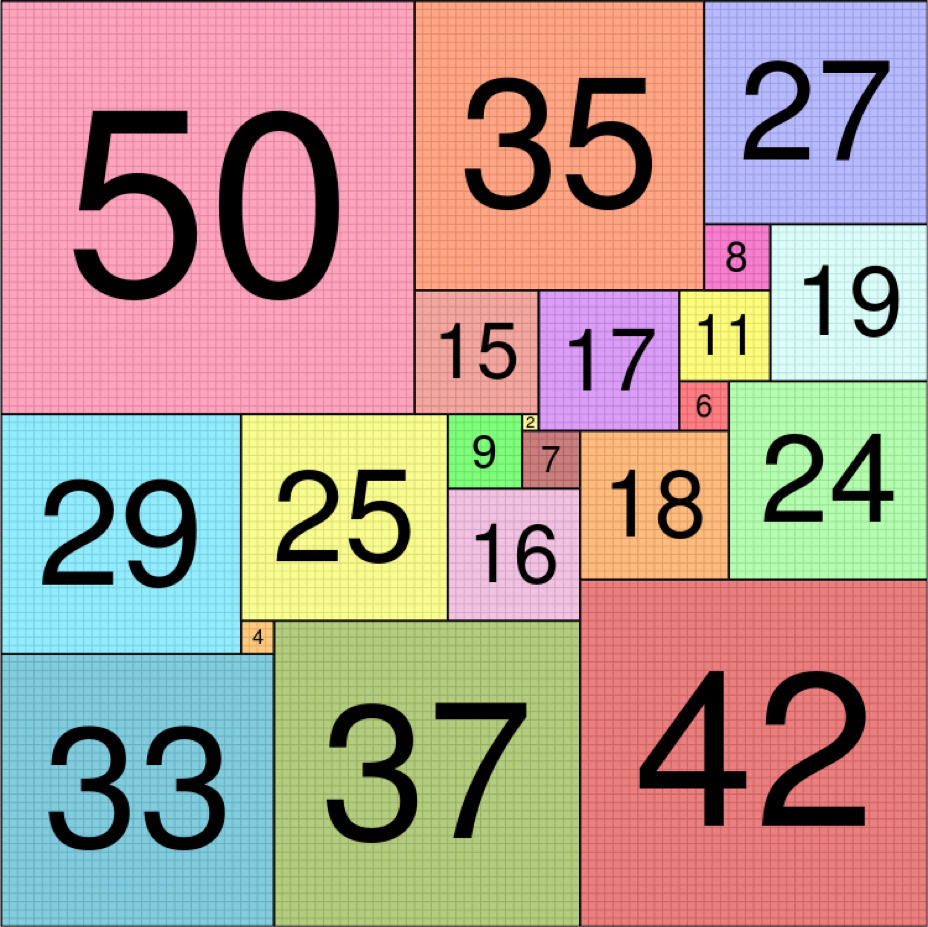
Quadrilaterals. You can cut a rectangle into five or more rectangles. Other authors have called this a "perfectly dissected rectangle", or “PDR” [3]. An interesting challenge is to find a five-rectangle PDR with dimensions that are ten distinct integers, with the largest number being as small as possible. 11 is possible, but 10 is not.
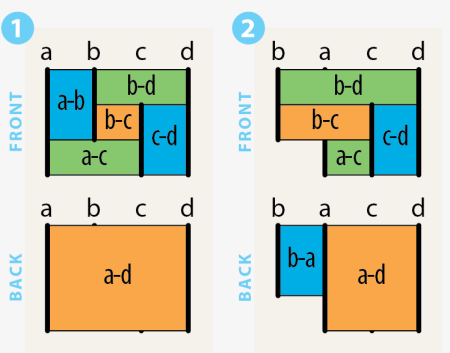
Hammocks. You can think of the rectangle cut into 5 rectangles as four vertical poles (labeled a,b,c,d at left) with hammocks hung between all 6 possible pairs of lines. The rectangles are labeled with the pair of lines they hang between. Notice that I count the whole rectangle as a sixth rectangle; you can think of the whole rectangle as the back side, and the other five rectangles as the front side.
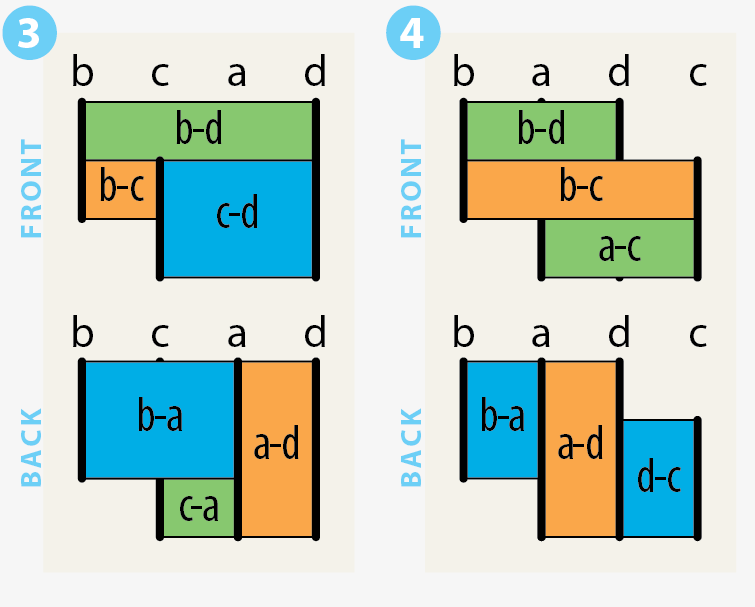
Slide the four “poles” left and right and you get different variations on the rectangled rectangle. For instance, if you swap the positions of line a and line b, as shown at left, the upper left blue rectangle rotates around to the back side of the construction. You can think of this construction as a shape that has been cut into two rectangles one way, and four rectangles in a different way, with all 6 rectangles maintaining a motley relationship. These constructions will turn out to be important when we move up a dimension to the boxed box later in this article.
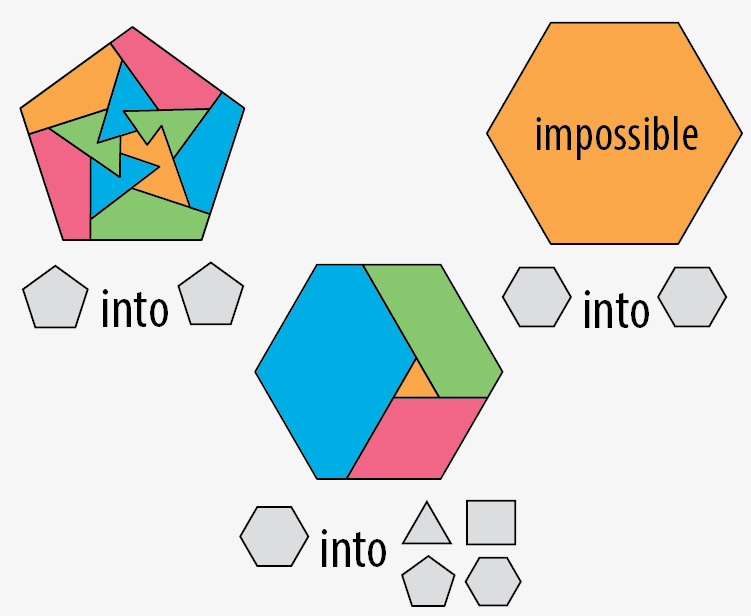
Pentagons. You can cut a pentagon into pentagons, some of which are concave. You can cut a hexagon into a triangle, quadrilateral, pentagon and hexagon.
Hexagons. After that, you’re stuck. You can’t (I believe) cut a hexagon into hexagons, a heptagon into heptagons, etc., for essentially the same reason you can't tile a sphere with hexagons. The proof is based on Euler’s formula for polyhedra, V-E+F=2, which relates the numbers of vertices, edges and faces in a polyhedron. (proof pending)
Relation to regular polyhedra
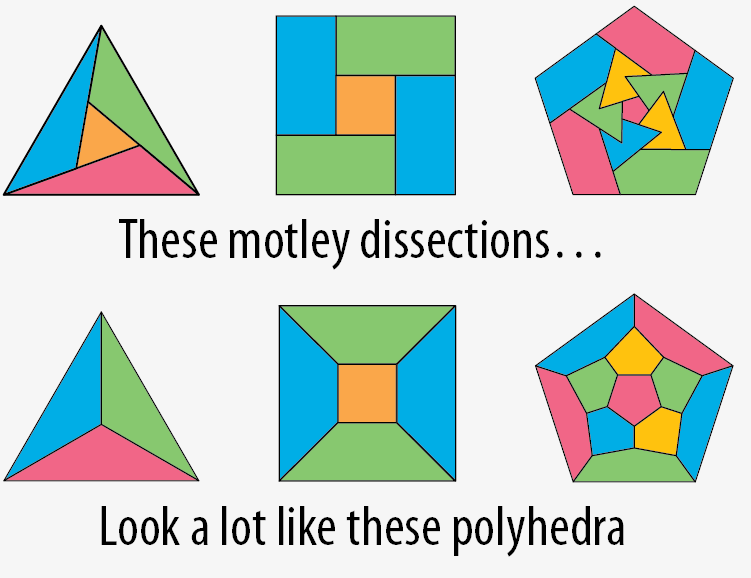
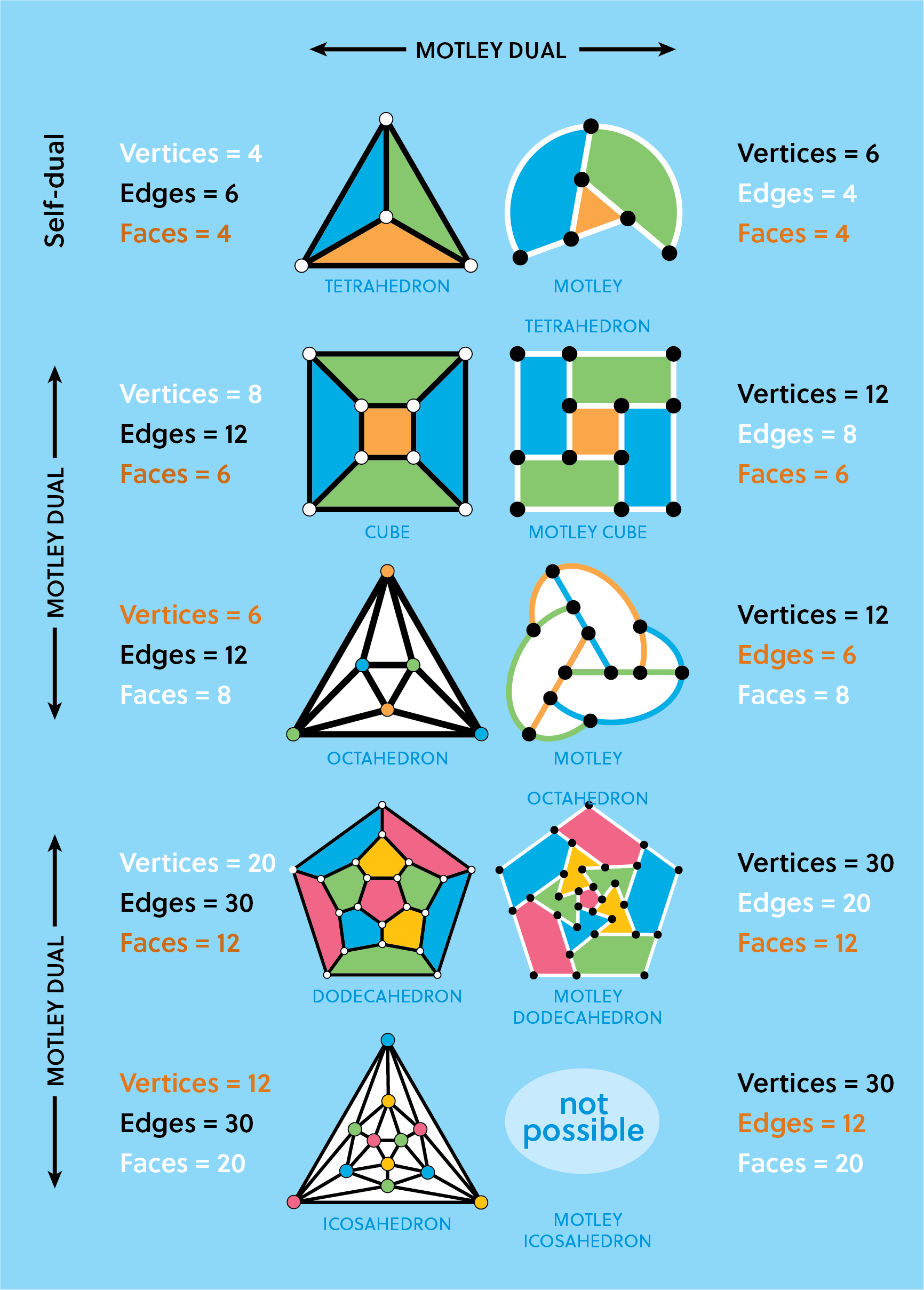
Polyhedra. The simplest motley dissections of the triangle into triangles, rectangle into rectangles, and pentagon into pentagons, shown at right, look suspiciously similar to the Schlegel projections of three regular polyhedra: the tetrahedron, cube and dodecahedron. What is going on here?
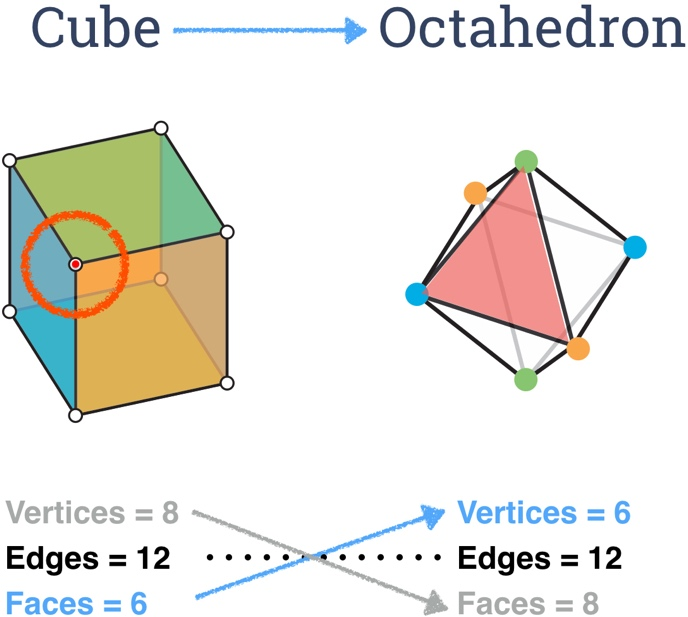
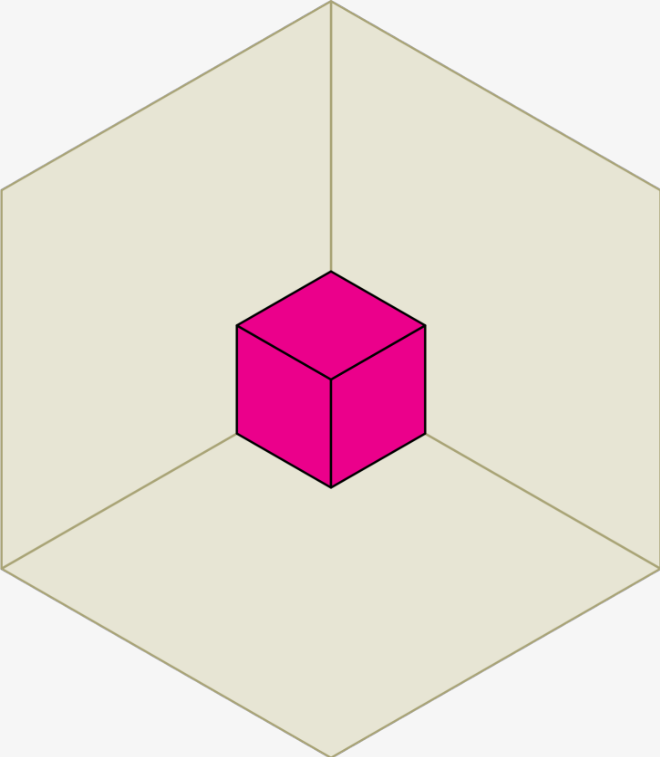
Duals. The “dual” of a polyhedron is the polyhedron created by mapping each vertex to a face, edge to edge, and face to vertex. Every polyhedron has a dual. For instance, the dual of the cube is the octahedron, as shown at right. Every relationship in the original polyhedron maps to an analogous relationship in the dual. For instance, every vertex of the cube is an endpoint of three edges, which maps to every face of the octahedron having three edges. Although the cube and octahedron are geometrically different, they have the same combinatorial structure, which geometer Branko Grünbaum calls an “abstract polyhedron” [6] — the graph structure in which vertices, edges and faces are abstract objects, and two objects (e.g. a vertex and a face) are connected by an edge (in the graph theory sense) if they are “incident” (e.g. the vertex is a corner of the face).
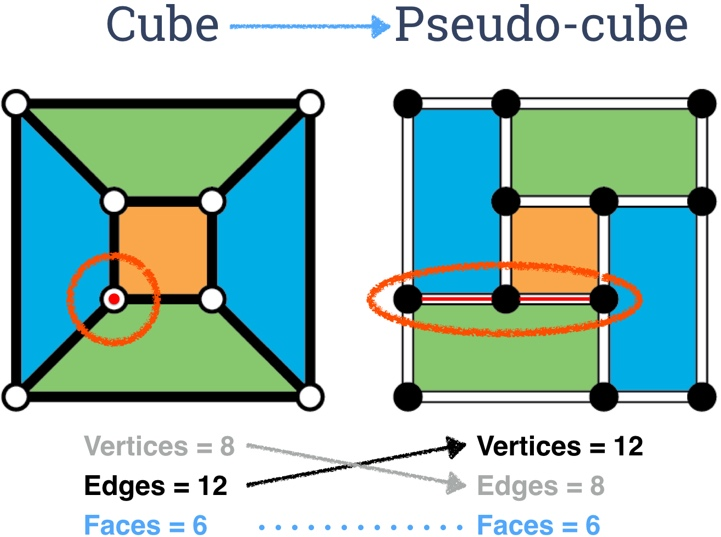
Motley duals. Interestingly, motley dissections also have a dual-like relationship to polyhedra, but with the roles of vertices and edges reversed. For instance, the cube is the “pseudo-dual” of the motley dissection of a rectangle into five rectangles, as shown at right. Check it out: the cube has 6 faces, 12 edges, and 8 vertices. The pseudo-cube has 6 faces, 8 edges, and 12 vertices.
Every face, edge and vertex of the cube maps to a face, vertex or edge of the pseudo-cube. For instance, the red vertex of the cube maps to the red edge of the pseudo-cube.
Each face of the pseudo-cube, including the whole shape, is a rectangle, each edge has 3, not 2 vertices, and each vertex is a corner of just 2 rectangles (a vertex does not count as a corner of a rectangle if it is situated in the middle of a longer straight side of the rectangle).
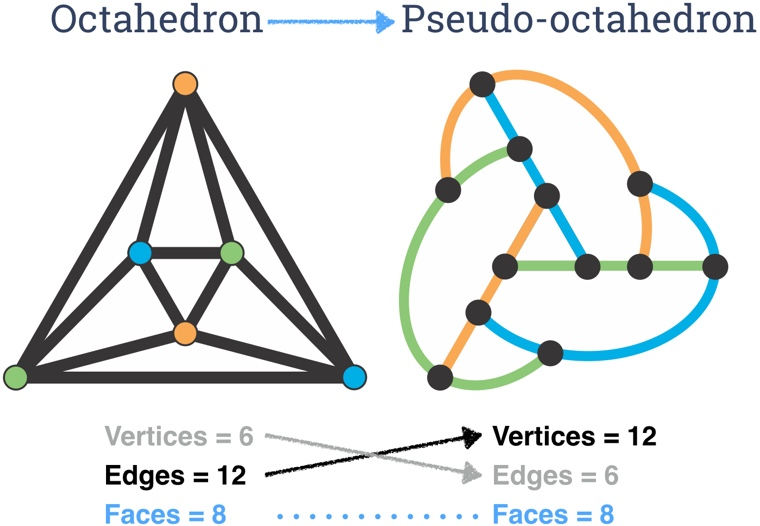
Pseudo-octahedron and pseudo-tetrahedron. As shown at right, the pseudo-dual of the octahedron is a motley dissection of a curvilinear concave triangle into 7 triangles, with 4 vertices along each edge.
And as shown below, the tetrahedron has two different pseudo-duals: a motley dissection of a curvilinear concave triangle into 3 triangles, and a motley dissection of a concave curvilinear digon (2-sided polygon) into 5 curvilinear digons.
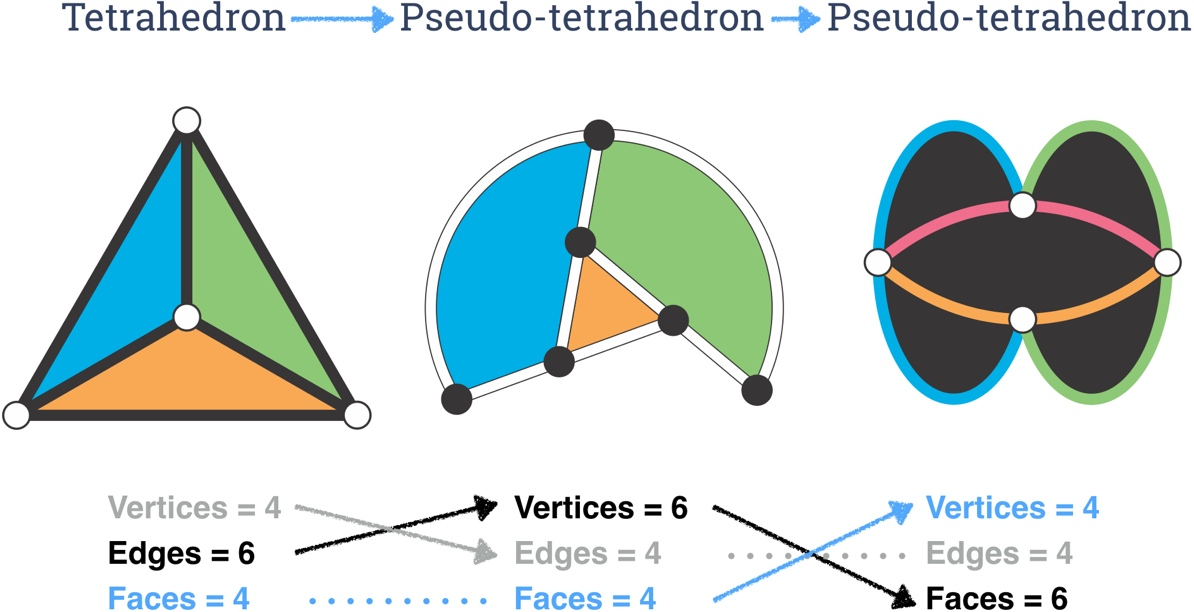
Of the other regular polyhedral, the dodecahedron has a pseudo-dual (the pentagon cut into pentagons, but the icosahedron, alas, does not have a pseudo-dual. (proof pending) Here is a complete list of the regular polyhedra and their pseudo duals.
4D polytopes
If the pseudo-dual of a 3D polyhedron is a 2D motley dissection, what is the pseudo-dual of a 4D polyhedron, aka polytope? I’m happy to report that four of the six regular 4D polytopes have pseudo-duals that are fine 3D motley dissections. You can find excellent descriptions and diagrams of the regular 4d polytopes in Hilbert and Cohn-Vossen’s book Geometry and the Imagination [5].
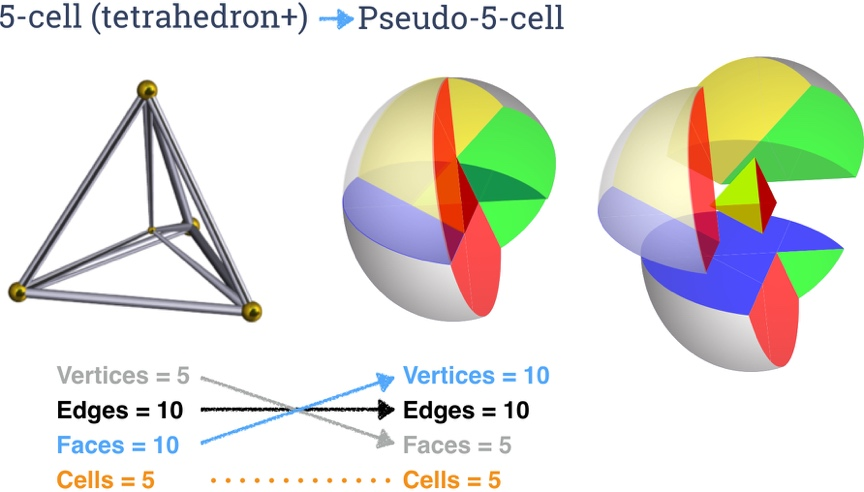
Pseudo 5-cell. The 5-cell is the 4D equivalent of the tetrahedron, with five tetrahedral 3-faces, 10 2-faces, 10 edges, and 5 vertices. At right are pictures of the five-cell and it’s pseudo-dual. In this relationship, the roles of vertices and 2-faces are reversed.
Like the pseudo-tetrahedron, the pseudo-5-cell is made up of curvilinear tetrahedra. Four planar pieces extend the faces of a central tetrahedron, and a fifth spherical 2-face wraps around the outside. Note that each of the 2-faces is itself a pseudo-tetrahedron, which is a motley construction involving 3 triangles on one side a 1 on the other, or 2 triangles on one side and 2 on the other.
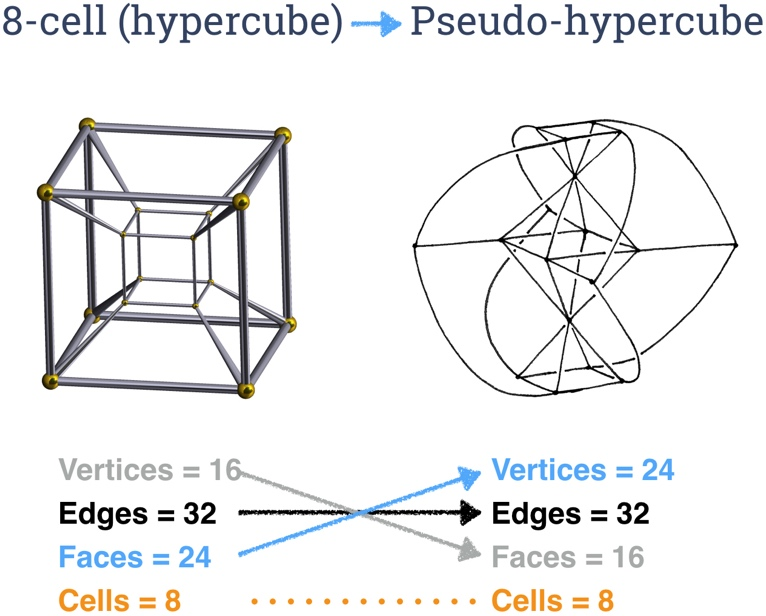
Pseudo 8-cell (pseudo-hypercube). The 8-cell, more commonly called the hypercube or tesseract, is a 4D solid bounded by eight cubes. In the pseudo dual, the eight cubical faces turn into eight octahedral faces, since the pseudo-dual operation maps 3-faces onto their conventional 3D duals.
The drawing at right of the pseudo-dual of the hypercube shows only half of the motley dissection of a curvilinear octahedron into 7 octahedron. In this drawing we see a central octahedron with flat planar faces. The eight triangular faces are extended outward in a pinwheel fashion to form eight curvilinear concave quadrilaterals. The various new curvilinear triangles form six half-octahedra, each with 4 triangular faces. Joining the eight exposed curvilinear edges to an inside out larger copy of the entire same figure completes the half-octahedra, for a total of 7 complete octahedra inside, and one concave curvilinear octahedron on the outside surface.
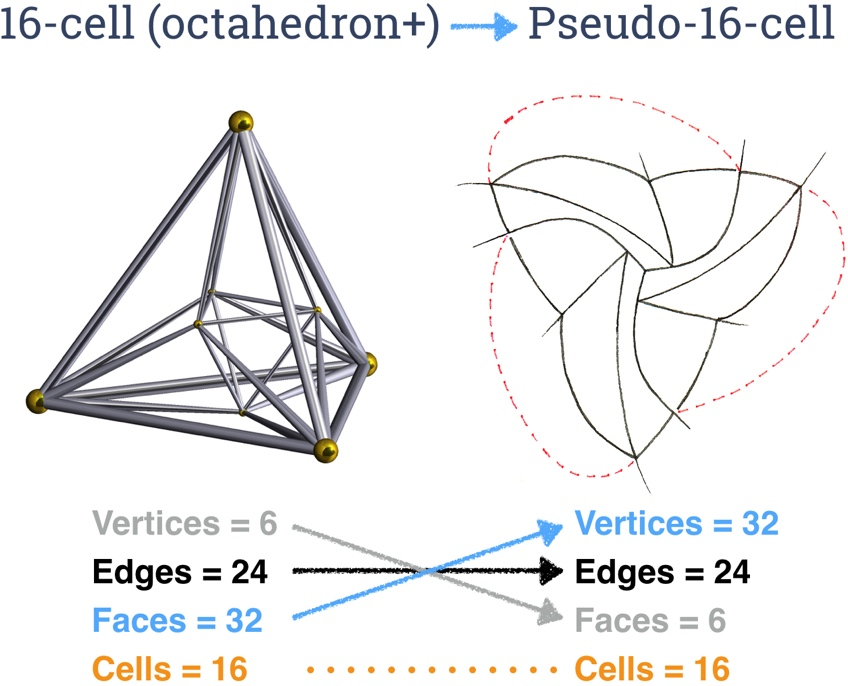
Pseudo 16-cell. The 16-cell is the dual of the hypercube, with 16 tetrahedral faces. Its pseudo dual is a motley dissection of a concave curvilinear tetrahedron into 15 curvilinear tetrahedra, bounded by a total of 8 planar components, each of which is a pseudo octahedron.
The drawings below show construction of the motley dissection. We start with a flat concave curvilinear hexagon, cut into 4 triangles. On this equatorial plane we build 1 tetrahedron the middle and 3 around it.
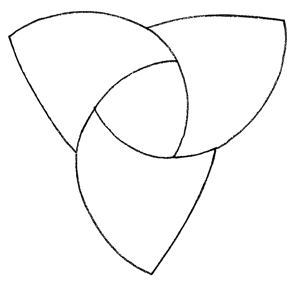
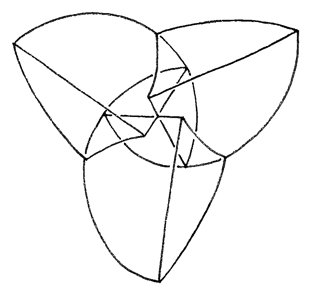
We add 3 small tetrahedra that act as dams in the valleys, then we fill the depression in the middle to the brim with 1 tetrahedron the points down, like water filling a triangular lakebed. Then we add three big curvilinear tetrahedra on top of the surface of this lake that leave only a small triangle of the lake showing in the middle. These 3 tetrahedra are like big claws…they start above the initial hexagon, then extend their talons through the plane of the hexagon to the other side. The red lines show where the talons pierce the plane of the hexagon; these lines are not edges of any of the tetrahedra.
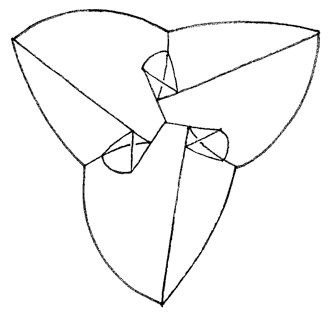
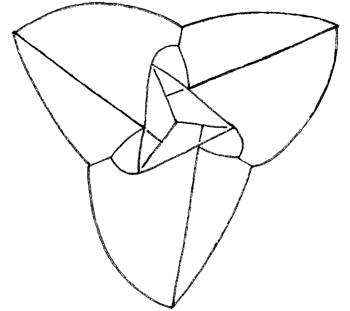
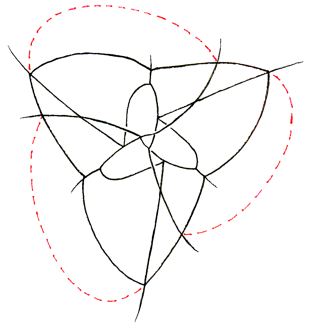
Now let’s peek below the equatorial plane. Again, we cut the curvilinear hexagon into 4 triangles, and attach 4 tetrahedra, hanging down from the plane. We complete the model by seeing the tips of the 3 claws reach under the equator and end at three points near the middle of the underside. That’s a total of 15 curvilinear tetrahedra, plus the outside surface, which is itself a concave curvilinear tetrahedron.
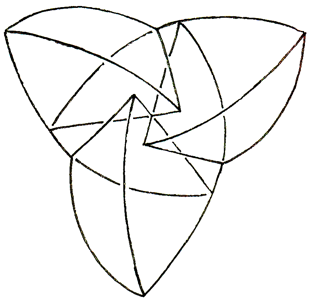
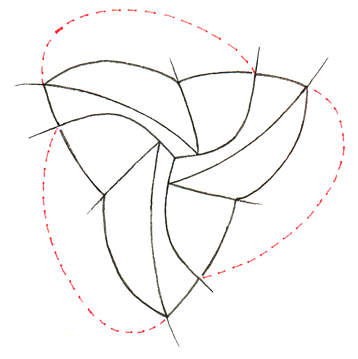
Note: these last two diagrams are the mirror image of what you would see if you looked up at the bottom of the model. I drew these diagrams so they align directly with the diagrams above. To translate these diagrams into their actual geometry, mirroring the shapes in your mind’s eye so they hang down from the equatorial hexagon, instead of rising up.
The boxed box: pseudo dual of the 24-cell
The most exciting moment in my investigation of motley dissections occurred when I considered the pseudo dual of the 24-cell.
The hypercube has cubical faces, which means its pseudo-dual has octahedral faces. The 24-cell — a wonderful unique self-dual polyhedron not directly analogous to a regular polyhedron in any other dimension —has octahedral faces, which means its pseudo-dual has cubical faces, or rather faces that are 6-sided rectangular solids, which I will call “boxes”.
And that meant to me that although the cubed cannot be cubed, it seemed likely that the box could be boxed, which is to say that a box (rectangular solid) can be dissected into a finite number of boxes such that no two boxes are bounded by the same two parallel planes in any of the three rectilinear directions, which means that the length, width and height of all boxes can all be chosen to be different numbers.
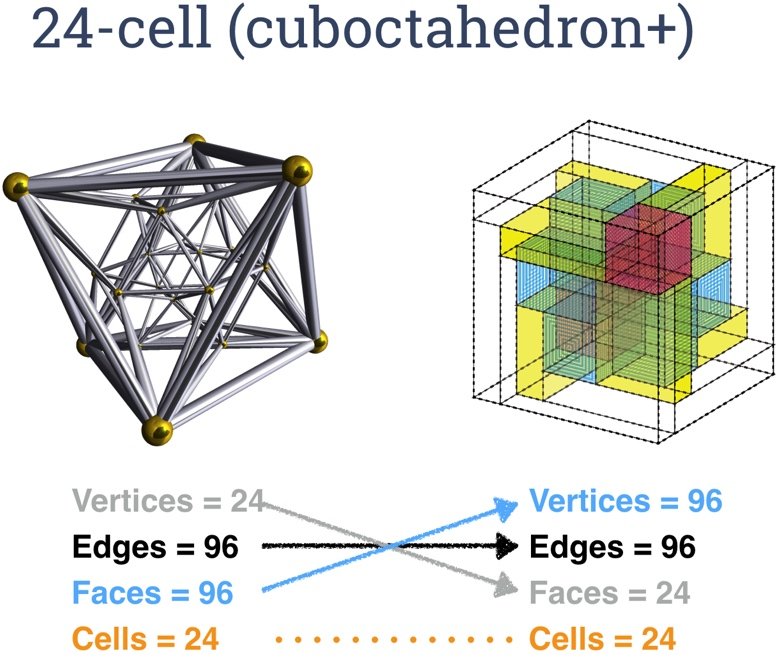
Armed with this intuition, I quickly found a motley dissection of a rectangular box into 23 smaller rectangular boxes. The construction is isomorphic to the 24-cell, with each of the 24 boxes (the whole box counts as one of the boxes) corresponding to one of the 24 octahedral 3-faces of the 24-cell, and each of the 24 planar faces of the boxed box corresponding to one of the 24 vertices of the 24-cell. (Remember that the 24-cell is self-dual, so it has the same number of 3-faces and vertices.)
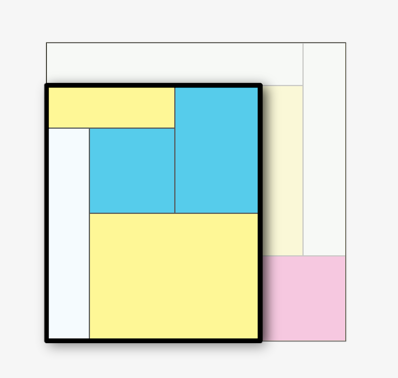
There are many combinatorially distinct boxed boxes with 23 boxes. In every such construction there are a total of 24 planar walls — 8 parallel walls or floors in each of the three orthogonal directions. Here are the 8 floorplans from one construction, starting with the ground floor and working upward. Think of the boxes as rooms in a house. Since no two rooms are bounded by the same two parallel planes, rooms that start on the same floor must always rise to different heights, topping out at different floors. Notice that each floorplan is itself one of the “hammock” constructions discussed earlier, created by shifting some of the edges of a rectangled rectangle.
The base (floor 1) of a boxed box must be a rectangled rectangle. On each rectangle sits a box.
Each of these five boxes rises to a different height. Floor 2 is the top of just one of these boxes.
Floor 3 is the top of two boxes: one starting from floor 1, and one starting from floor 2.
Floor 4 is the top of three boxes starting from floors 1, 2, 3, and the bottom of three more boxes,
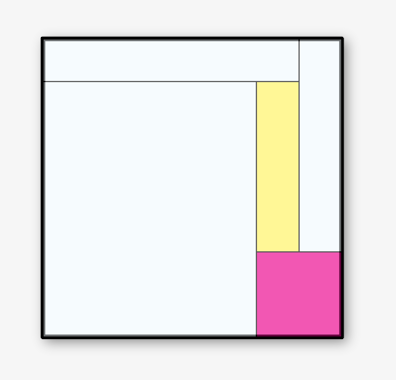

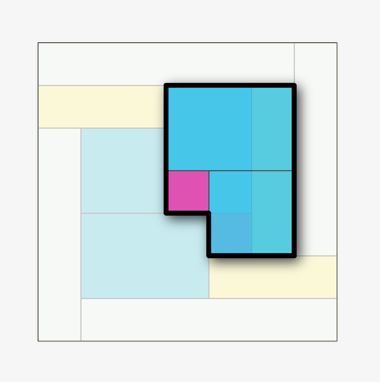
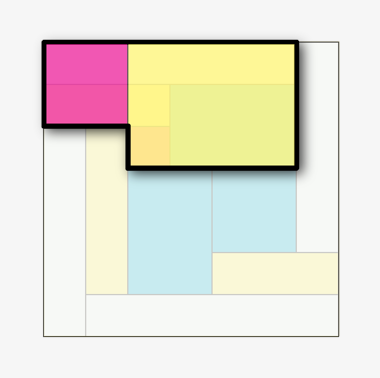
Now the pattern repeats in reverse. Floor 5 is the top of three boxes, and the bottom of three.
Floor 6 is the top of 4 boxes and the bottom of two.
Floor 7 is the top of 5 boxes and the bottom of one.
The roof is the top of 5 boxes, and also the top of the whole box.



Because I love symmetry, I look for and found a construction with 6-fold 3-bar symmetry — the highest possible degree of symmetry for such a construction. Here is the construction built up from one corner of the bounding cube to the other, emphasizing the 3-fold rotational symmetry. We start in one corner, with a 2x2x2 cube. We cover that with 6 boxes in 2 sizes, which spin around it in 3-fold rotational symmetry.
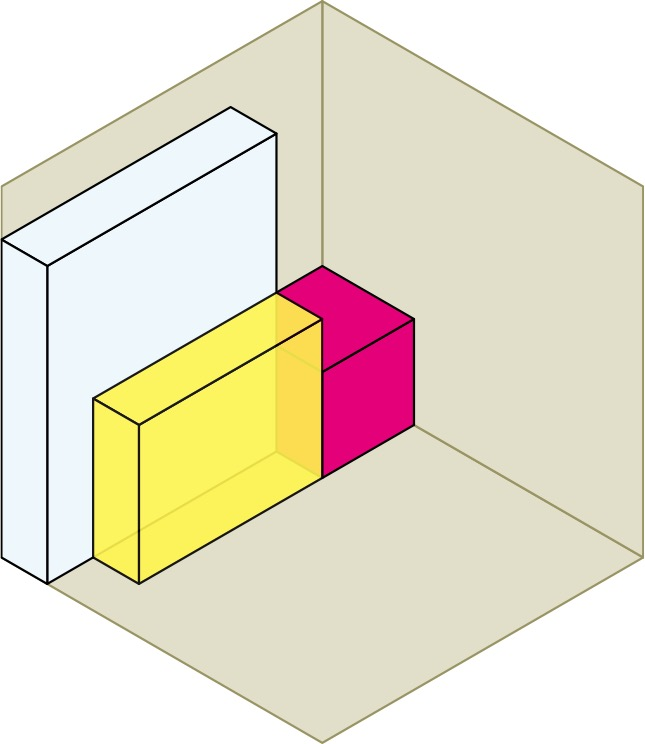
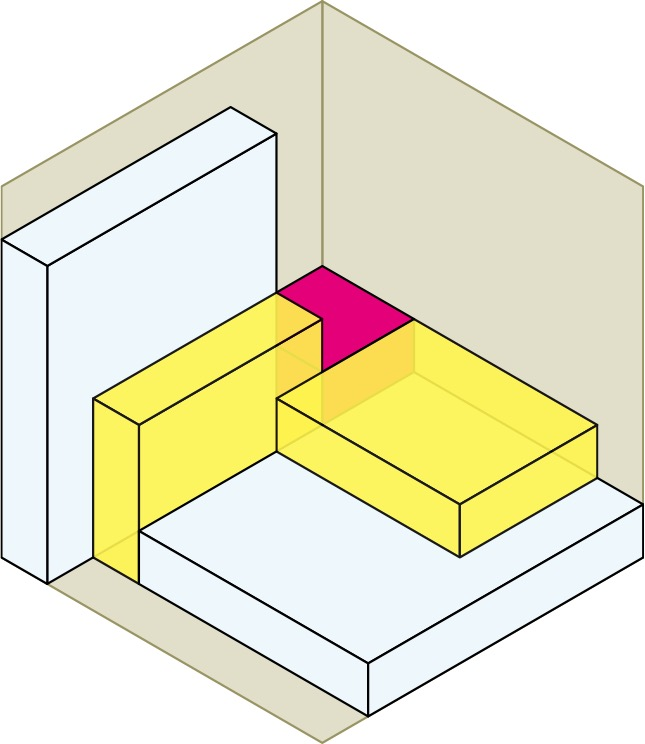
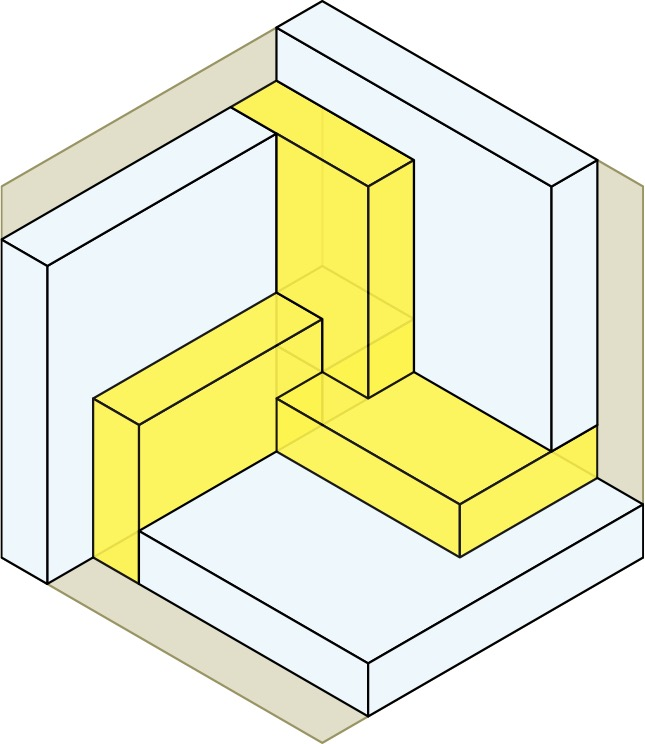
Next we place the second of 5 cubes that go up the main spatial diagonal. This cube is 1x1x1, and it is surrounded on the 3 back faces by yellow boxes, and on the 3 front faces by 3 blue boxes. Then we place the third cube in the center of the whole construction and surround it by 3 more blue boxes, which are twisted mirror images of the first 3 blue boxes. We are now into the second half of the construction.
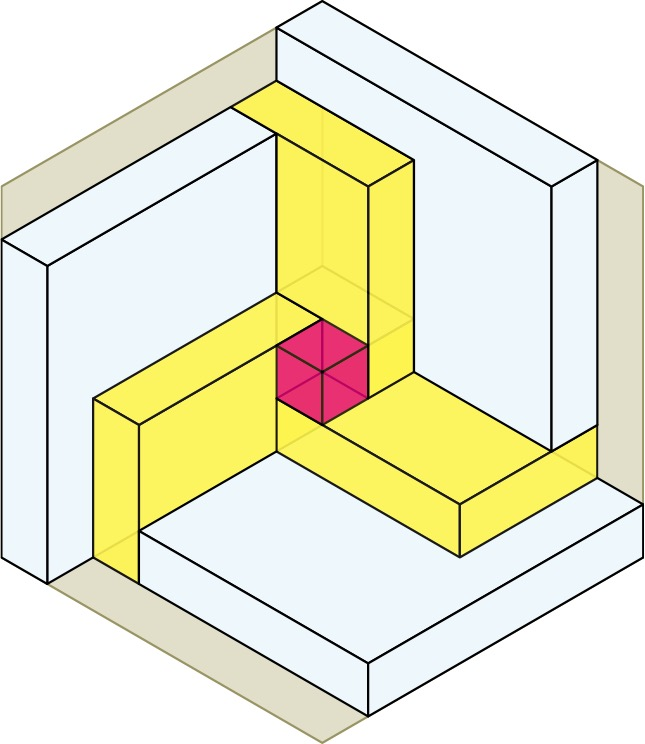
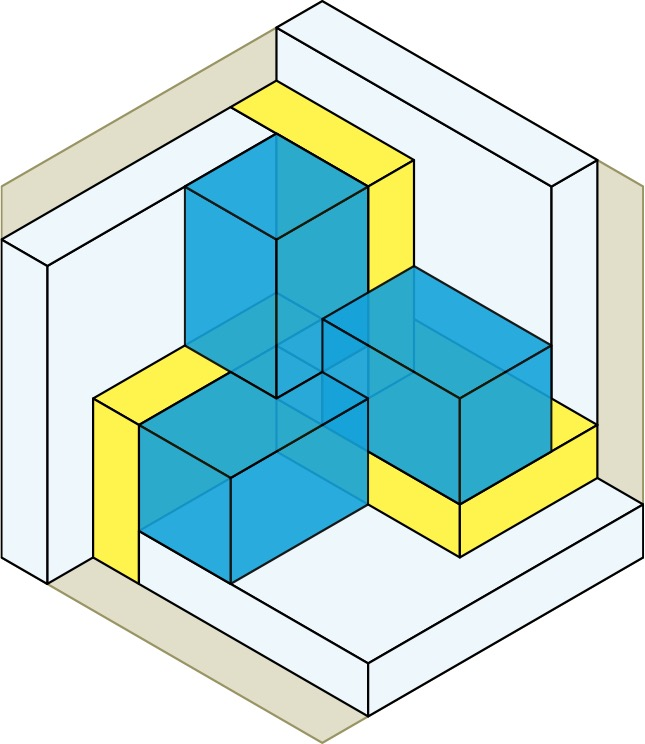
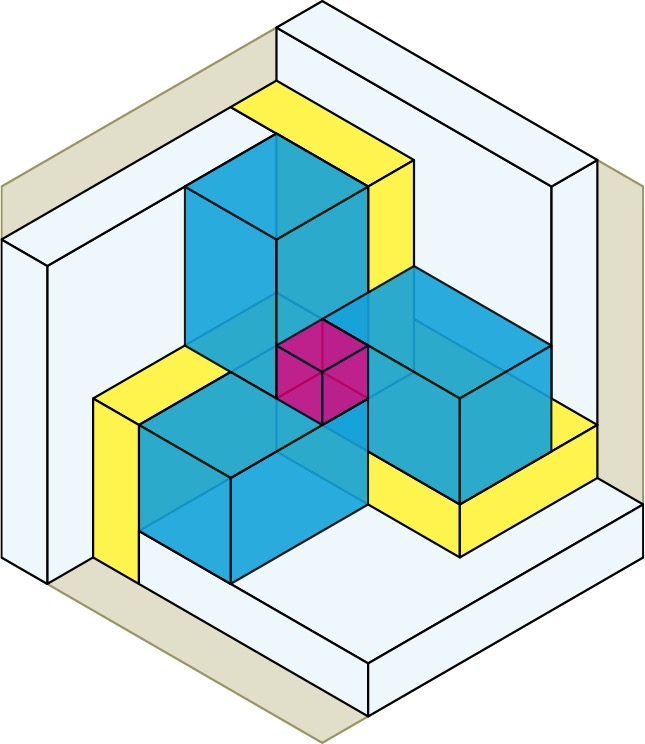
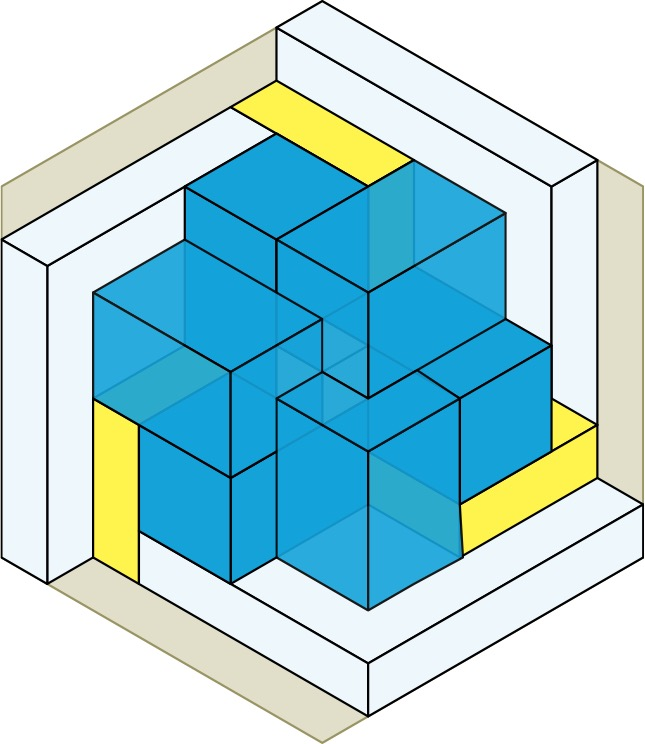
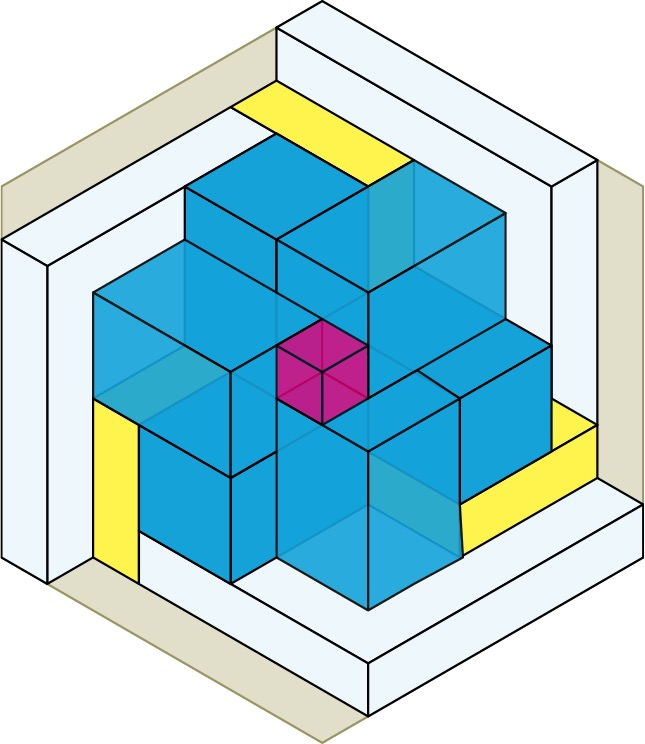
We place the fourth cube an cover it with 3 more yellow boxes, which are twisted mirror images of the first 3 yellow boxes. Finally we complete the whole cube by placing 3 more white boxes and a fifth and final cube. In total, there are 6 cubes (5 red + the whole cube) + 6 white boxes + 6 yellow boxes + 6 blue boxes = 24 boxes (23, if you don’t count the whole cube).
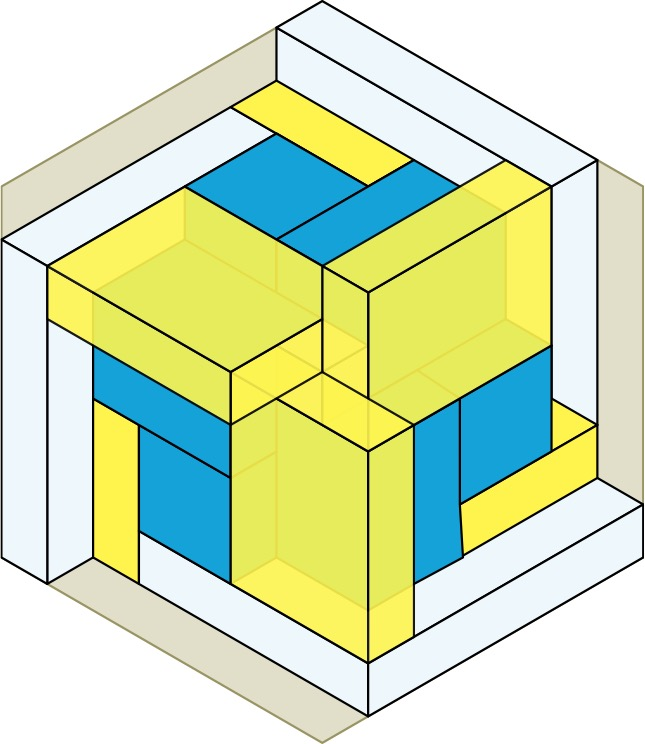
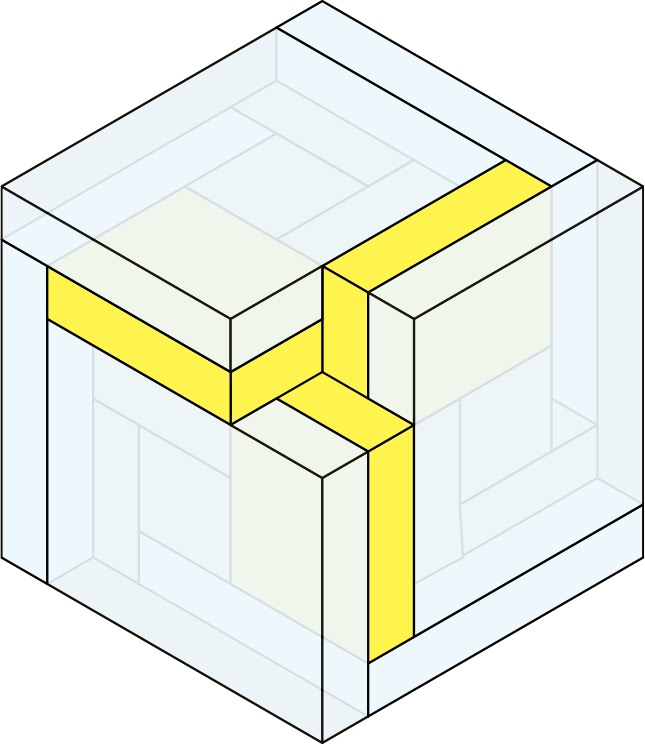
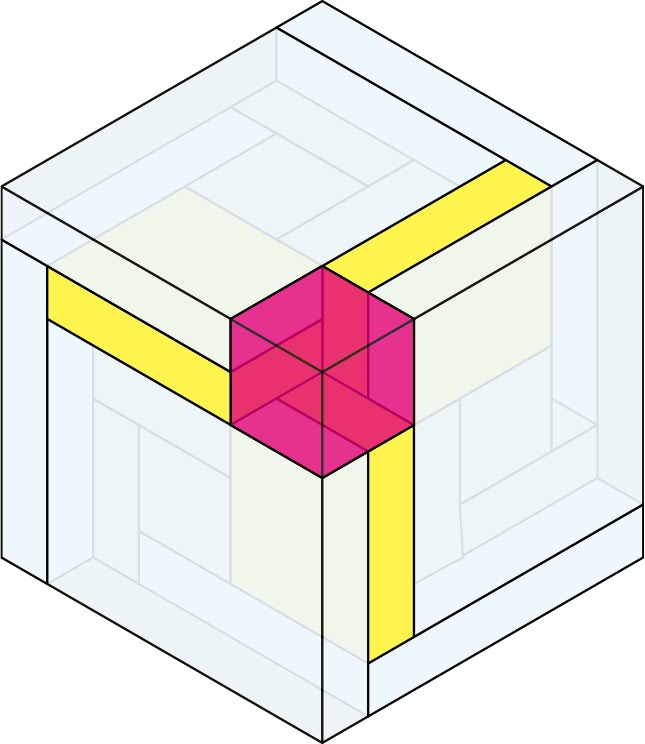
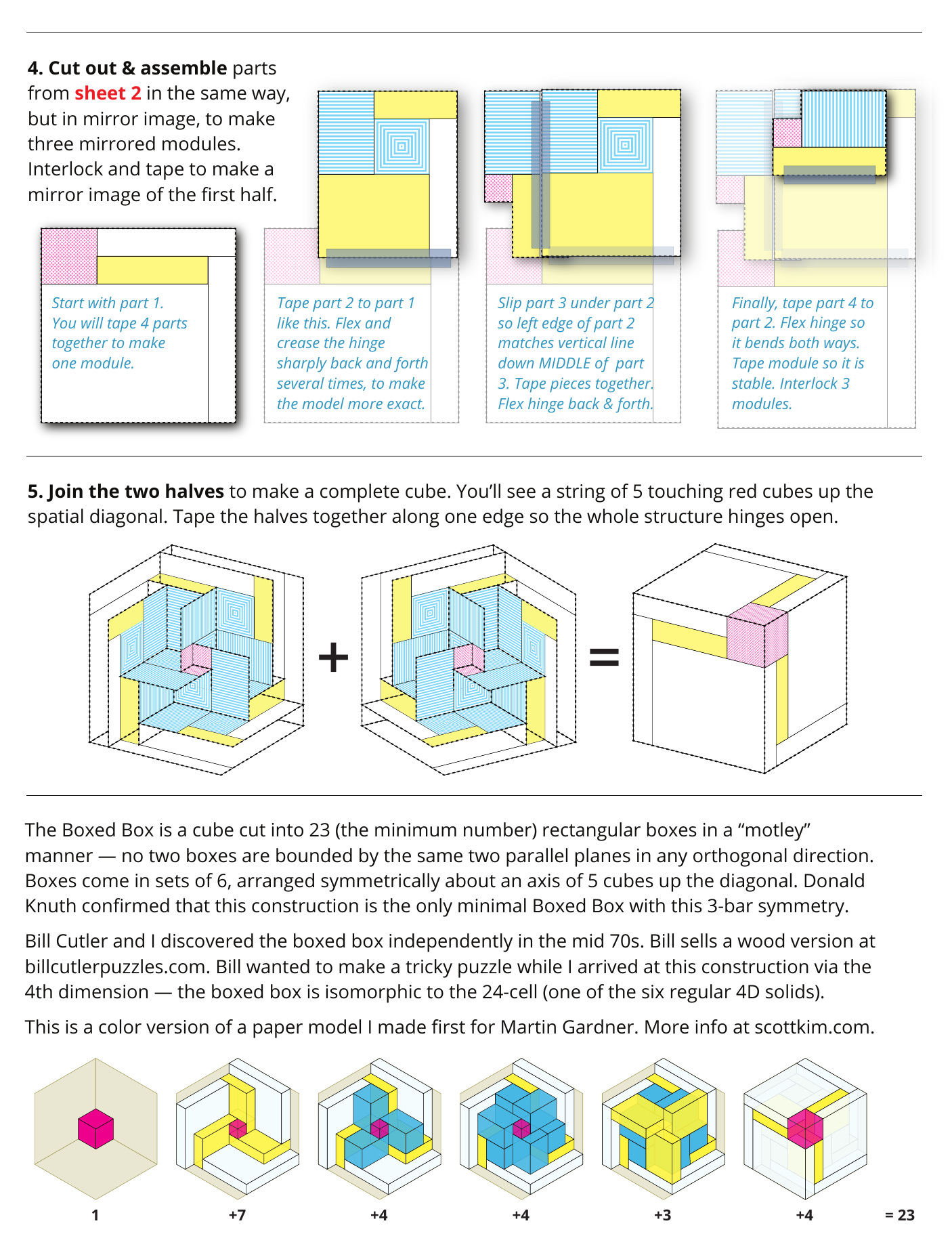
Paper Model
Paper model. When I wrote Martin Gardner about the boxed box, I included a paper model of the Boxed Box, which came apart into 6 congruent units that folded flat. The component parts and the assembly sequence are shown on the next page. I included a transparent colored version of this model in the G4G13 gift bag.

Bill Cutler. Gardner wrote me back to tell me that mathematician and puzzle maker William Cutler had simultaneously discovered the same idea, albeit by different means, without the detour into the fourth dimension or relating motley dissections to polyhedra. In Cutler’s version, all 72 dimensions of all 24 boxes (including the whole box) are different sizes. Cutler wrote up his discovery in the Journal of Recreational Mathematics, [6]. Cutler sells a wooden version of his construction, shown at left.
Donald Knuth. In 2017 my PhD advisor and Stanford computer scientist Donald Knuth surprised me with the news that my construction was the only possible boxed box with 3-bar symmetry. I had not published my construction; he had dug up my correspondence with Gardner, and written a program to confirm uniqueness, and used his discovery as an exercise in the most recent chapter of his magnum opus The Art of Computer Programming [7]. Knuth once told me half-seriously that finding the right name for a project is half the work. So after all these years he was the one to give my dissections a name, and call them “motley dissections”.
References
- Gardner, Martin. Mathematical Games column of Scientific American, pp. 136-142, Nov. 1958
- W. T. Tutte, Squaring the Square, Canadian Journal of Mathematics, 11:2, pp. 197-209, 1950.
- A. Yao, E. Reingold, and B. Sands, Tiling with Incomparable Rectangles, Journal of Recreational Mathematics, 8:2, pp. 112-119, 1975.
- Grünbaum, Branko. Are your polyhedra the same as my polyhedra?, Discrete and Computational Geometry: The Goodman-Pollack Festschrift. B. Aronov, S. Basu, J. Pach, and Sharir, M., eds. Springer, New York 2003, pp. 461 – 488.
- Hilbert, David and S. Cohn-Vossen. Geometry and the Imagination. AMS Chelsea Publishing, 1999.
- Cutler, Bill, and Scott Kim. Subdividing into completely incongruent Boxes, Journal of Recreational Mathematics, 12:2, pp. 104-111, 1979-80.
- Knuth, Donald. The Art of Computer Programming. Addison-Wesley, 2011.
Instructions for the paper model of the Boxed Box.